Forme canonique

[mari2]

Bonjour, j'ai un problème pour trouver la forme canonique d'une équation.
En fait je n'ai pas la technique ou du moins je ne la connais pas si quelqu'un peux me donner un coup de main ça serai gentil Merci.
Voici un exemple:
x²-2x+y²-4y=0<=>(x-1)²-1+(y-2)²-4=0 Comment a t-on fait pour trouver cela ?

[Clembou]

[Edit pour la modération] J'espère que mon message respecte les régles en vigueur sur le forum[/edit]
EDIT de la modération : oui c'est bon.

Soit l'équation :



On veut la mettre sous la forme canonique donc sous la forme :



Première étape, tu regardes les termes en



Tu remarques que c'est le début d'une identité remarquable . Manifestement ici, on a : et . Donc :



Deuxième étape : on regarde maintenant les termes en et on fait pareil qu'à l'étape 1.



Dernière étape : on fait la somme de ce qu'on a trouvé et le tour est joué.


Pour t'entrainer, mets sous la forme canonique :



où est un paramètre...

Bon courage !

[Alex75000]

x²-2x+y²-4y=0<=>(x-1)²-1+(y-2)²-4=0

c'est simple, pense à l'identité remarque (a-b)²=a²-2ab+b² pour ton x ici

x²-2x en prenant a=x et b=1, on obtient (x-1)²=x²-2x+1

or dans ta forme on a juste x²-2x il suffit donc de soustraire 1 d'où:

x²-2x=(x-1)²-1

pour ton y tu fais de meme en faisant (y-2)²

[sb30]

Bonjour,
je ne sais pas si c'est la bonne technique mais personnellement j'aurais utiliser "l'art d'écrire zéro", cad : on écrit x²-2x = x²-2x +1 -1 de façon a faire apparaitre une identité remarquable et ensuite on factorise ...

[Clembou]

Bonjour,
je ne sais pas si c'est la bonne technique mais personnellement j'aurais utiliser "l'art d'écrire zéro", cad : on écrit x²-2x = x²-2x +1 -1 de façon a faire apparaitre une identité remarquable et ensuite on factorise ...

Pourquoi pas ! C'est une autre méthode pour découvrir l'identité remarquable...

[mari2]

Je comprend la technique mais je bloque un peu avec le 9 dans E1.

[Ericovitchi]

D'abord il faut toujours avoir en tête
ou

Si tu vois un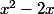 dans une formule par exemple tu peux toujours te dire "tiens c'est le début de " mais si j'écris ça alors je vais créer un +1 en plus donc il faut que je compense en ajoutant un -1 derrière :

Alors évidemment, c'est pas toujours évident. Prenons un exemple dur. Si tu trouves un ça peut laisser perplexe.
Mais en fait c'est pareil :
je te fais exprès apparaître un avec un a qui vaut x et un b qui vaut 3/4


l'autre mécanisme de factorisation classique est lorsqu'il faut factoriser un truc comme Si tu as repéré que en remplaçant x par 1 ca faisait zéro, tu te dis que l'on pourra mettre (x-1) en facteur
Alors tu poses
et tu te dis : pour fabriquer mon
il faut que je mette un x :
mais en mettant un x, je fabrique bien un mais je fabrique aussi un -x or dans mon équation je n'ai pas un -x, j'ai un +x, donc il faut que je fabrique un +2x pour compenser
et ouf mon -1 par 2 redonne bien ma constante -2

[mari2]

Ok j'ai compris mais par exemple avec 4x²+9x+6y-9y²=0
Le 9 me pose problème.

[mari2]

ha j'ai trouvé, (2x+(9/4))²=4x²+9+(9/4)² ? est-ce bon ?

[Ericovitchi]

non je ne te suis pas bien, tu avais 4x²+9x+6y-9y²=0
donc effectivement c'est un
ça crée bien le 4x². Pour fabriquer le 9x il te faut un truc b qui fasse que
2 . 2x. b = 9x donc ton b c'est 9/4

Ca fait donc mais en faisant ça, tu fabriques un 81/16 qui n'existe pas donc il faut compenser en rajoutant un -81/16

et au total

Fais pareil avec les y pour voir si tu as tout compris ?

[mari2]

Ok merci c'est ce que j'ai trouvé.

[Ericovitchi]

Mouais, montres moi ce que tu as fait des y qu'on vérifie ça ?

[mari2]

je trouve -(3y-1)²-1. c'est bon ?

[sb30]

je trouve -(3y-1)²-1. c'est bon ?

petite erreur de signe pour la valeur à rajouter, mais tu semble avoir pris le coup.

[mari2]

ha oui c'est vrai Merci.