Fonctions polynome : exercice incompréhensible ... je panique!

[tekticlem]

je trouvais bizarre aussi le 1225.. Mais oui je ne comprends pas pk on laisse 900 ? je croyais qu'on calculait alpha et beta a partir de la fonction donnée moi..

[Adoration_For_None]

je trouvais bizarre aussi le 1225.. Mais oui je ne comprends pas pk on laisse 900 ? je croyais qu'on calculait alpha et beta a partir de la fonction donnée moi..

Je sais qu'il y a des formules pour avoir les formes canoniques, moi je t'ai fais le truc à l'ancienne, la méthode calculatoire.
Pour le 900 je le laisse dehors, parce qu'il fait pas parti d'un début de développement de carré. Si tu veux tout ce qui est nombre et qui comporte pas de x, donc d'inconnu je le laisse en dehors de ma factorisation.

[tekticlem]

oki mais malheureusement j'ai une prof tres "casse-coui***" (exuse l'expression) qui veut tout justifier et si on utilise pas la méthode donc si on ne justifie pas correctement, c'est zéro ... Oui ma prof est un cas ! Désolé mais je comprends vraiment pas ta méthode.. :P

voila comment ma prof nous a apprit a calculer une forme canonique :

a(x-A)² + B, calculer d'abord A = -b/2a puis B = P(A)
Ce que je comprends pas c'est que j'ai tout fait comme elle le veut et je trouve quand meme 1225 à la fin :/ t'en ai sure et certain qu'on laisse le 900 ?

[Adoration_For_None]

Hum alors on va faire plusieurs choses.

1. Si tu veux vérifier ta forme canonique tu calcules l'image d'un x quelconque par la fonction f de départ et avec ta forme canonique. Si tu tombes pas sur la même chose tu as faux.

2. Alors dans sa méthode .
Et .
Ainsi la forme canonique est -

Ce qui est très intéressant personne trouve pareil, et rien n'est juste dans ce qu'on a proposé !

[tekticlem]

mdr bah si, ce que tu as fais en dernier, ça à l'air d'etre juste, non ?

[Adoration_For_None]

C'est juste qu'en apparence ! x) Ca donne pas les mêmes résultats.. :/
Dans ma première méthode, j'ai fais une erreur de calcul je vais rectifier dans mon post et voir si ça marche. :)

[tekticlem]

moi j'ai verifier mon premier calcul et c'est faux, je trouve -2x² -110x - 4825, c'est meme extremement faux ...

[Adoration_For_None]

Erreur de calcul corrigé dans mon post [la méthode que tu comprends pas] et ça marche !! :D

[tekticlem]

J'ai recalculer et j'ai trouvé : f(x) = -2(x-55/2)² + 1225/2, ça me parait un peu plus juste, je vais vérifier si c ça !

[Adoration_For_None]

Oui c'est ça :) J'ai trouvé la même chose avec ma méthode. :)

[tekticlem]

ah ouais ?? mais j'ai verifier et ça marche pas :/ Quand je redeveloppe ça me donne : -2x² +110x - 1800, pas toi?

[Adoration_For_None]

J'ai pas vérifié comme ça. Dans un tableur, j'ai rentré une colonne de x, une colonne qui calcule f(x), et une colonne qui calcule f(x) avec la forme canonique.
J'obtiens ceci :



Ainsi on obtiens sur [0;30], la même image. Donc on peut supposer que les deux expressions sont équivalentes.

Puis en développant je tombe bien sur la même expression.

[tekticlem]

Ah ouaaaais ! oki :) Bon bah niquel ! et t'as trouver le b?

[Adoration_For_None]

Alors, pour justifier ton tableau de variation, c'est tout bête, il faut pas se contenter de balancer le tableau comme un cheveux dans la soupe
Il faut calculer l'abscisse du sommet de la parabole qui est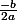 , ça doit être dans ton cours.
Ou sinon de manière moins catholique, comme tu sais que la représentation d'un trinôme est une parabole donc une courbe symétrique, tu peux avancer que l'abscisse du sommet de la parabole et le milieu des racines, ainsi .
Avec la première formule on a .
Et avec la seconde tu as
Ou sinon simplement comme ta forme canonique est -, tu dis que l'abscisse du sommet c'est A, donc . Bref, tant de méthode pour trouver l'abscisse du sommet de la parabole.

Après tu sais que la variation d'un trinôme dépend du signe de a, si a0.
Donc ici tu appliques à ton trinôme qui est pour rappel -.
Et après tout ça tu peux tracer le tableau.

Remarque : En méthode je te conseille d'utiliser celle avec la forme canonique. Comme ça elle ne sert pas à rien.

[tekticlem]

De mon coté pour le b, je vais d'abord calculer delta, puis voir le nb de solution, normalement c'est une, ensuite je vais dresser un tableau de variation qui commence a 0 et qui finit a 50 en faisant aparaitre la seule solution au milieu ... c'est ça tu penses?

Ce qui me pose problème c'est comment justifier le tableau de variation avant de l'avoir fait ... ?

Ah je viens de voir ta reponse, attends je la lis :)

[Adoration_For_None]

Par contre oui très bonne remarque fais ce tableau uniquement sur [0;50] vu que d'après l'énoncé 0

[tekticlem]

Ah oui et l'abscisse du sommet de alpha, c'est beta non?

[Adoration_For_None]

Je vois ce que tu as voulu dire, donc je vais te répondre oui. :)
Mais dit plutôt que beta est l'image de alpha par le trinôme, ainsi alpha est l'abscisse du sommet et beta l'ordonnée du sommet, tu vas d'ailleurs t'en servir de cette ordonnée pour la question c ! :)

[tekticlem]

C'est bon je l'ai fais :) Peux tu m'aider pour le c ? Apres fini, je vais dormir, je te laisse tranquil ;) Meme si j'ai d'autres exercices, je me debrouillerais et je les ferais un autre jour de toute façon ...

[Adoration_For_None]

Comme je l'ai dit dans mon post précédent : beta correspond à l'ordonnée du sommet de la parabole. Or en ordonnée on nous présente les bénéfices et abscisse la quantité de farine. Donc pour que les bénéfices soit maximum, on doit produire alpha tonnes de farine, et on gagnera beta €.