Fonctions exponentielles

[zygomatique]

Ok merci. Dans la question les parenthèses sont comme ça:
Pour tout nombre réel x, on pose :

f(x) = e^-x + e^-x le tout divisé par 2 et
g(x) = e^-x - e^-x le tout divisé par 2.

Démontrer que pour tout nombre réel x, on a : (f(x))² - (g(x))² = 1

non seulement elle ne connait pas la règle sur les exposants mais en plus elle ne connait pas les parenthèses ....

f(x) = (e^-x + e^-x)/2

g(x) = (e^-x - e^-x)/2


ensuite c'est évidemment pas l'énoncé ... (a + a)/2 = a ...


et inutile de citer le msg précedent à chacune de tes réponses

heu ... y a quequ'chose qui tourne pas rond ... ou vous ne savez pas lire ...

il est évident que

il est fort probable que l'énoncé est :



et c'est une évidence si/quand on connait les cosinus et le sinus hyperbolique ... mais bien sur je ne reproche pas de ne pas le savoir au lycée !!!


IL EST INUTILE VOIRE MËME STUPIDE DE CITER LE MSG PRECEDENT A CHAQUE REPONSE !!!!!!!!!!!!

[Laaure02]

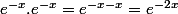
Ok mais dans l'exo c'est pas une multiplication mais une addition

oui, je sais ! Je vais t'écrire proprement le développement :



. . . où alors, il y a quelque chose qui m'a échappé . . . ! ? . . .

Merci c'est gentil mais je pense que tu t'es trompé car la consigne de l'exercice est démontrer que (f(x))² - (g(x))² = 1 . Le résultat doit donc obligatoirement être égal à 1 ....

[zygomatique]

MDR

et en plus elle ne sait pas lire ...

[laetidom]

Salut @ tous !,

On doit démontrer que la différence des carrés conduit à 1, le résultat doit être = 1 si en amont on a un énoncé " nickel chrome " et sans erreur . . . on est donc dans l'expectative . . .

[Laaure02]

Bonjour,
J'ai demandé ma prof de maths et elle s'est trompé dans l'exercice ! (PS: zygomatique → je sais très bien lire merci !!! C'était tout simplement la prof qui s'était trompé !)
Merci pour ton aide laetidom. J'ai de ce fait réussi à faire l'exercice.
Bonne journée

[laetidom]

Bonjour,
J'ai demandé ma prof de maths et elle s'est trompé dans l'exercice ! (PS: zygomatique → je sais très bien lire merci !!! C'était tout simplement la prof qui s'était trompé !)
Merci pour ton aide laetidom. J'ai de ce fait réussi à faire l'exercice.
Bonne journée

Merci pour l'info Laaure, juste, peut-on connaître l'énoncé corrigé ? ça peut intéresser d'autres élèves . . . c'est aussi ça l'esprit d'un forum, merci pour ta compréhension Laaure et bonne journée @ toi !

[Laaure02]

Oui bien sur je le donne après là je vais en cours.
Bonne journée également

[laetidom]

Oui bien sur je le donne après là je vais en cours.
Bonne journée également

Merci Laaure pour ta compréhension et bon cours !

[Laaure02]

Pas de souci !
Alors voilà le bon énoncé :

f(x) = e^x + e^-x /2
g(x) = e^x + e^-x /2

Démontrer que pour tout nombre réel x, on a : (f(x))² - (g(x))² = 1.

[Lostounet]

Pas de souci !
Alors voilà le bon énoncé :

f(x) = e^x + e^-x /2
g(x) = e^x + e^-x /2

Démontrer que pour tout nombre réel x, on a : (f(x))² - (g(x))² = 1.

Ce serait plutôt: g(x)=( e^x - e^(-x))/2
Le plus simple pour prouver que f(x) ^2 - g(x)^2=1:

que vaut f(x)+g(x) ?
Que vaut f(x)-g(x) ?

Donc que vaut (f(x)+g(x))*(f(x)-g(x)) ?
Conclusion?

[laetidom]

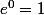
Effectivement, maintenant le résultat fait bien , et comme tu as réussi à le faire tout est donc ok Laaure ! Bonne soirée.

[Laaure02]

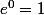
Effectivement, maintenant le résultat fait bien , et comme tu as réussi à le faire tout est donc ok Laaure ! Bonne soirée.

Oui c'est bon. Merci pour ton aide !
Bonne soirée à toi aussi.

[laetidom]

Oui c'est bon. Merci pour ton aide !
Bonne soirée à toi aussi.

Contents d'avoir été utile ! Bonne soirée et @+ sur le forum !