Fiction reciproque
7 messages
- Page 1 sur 1
Re: Fiction reciproque
bonjour,
=\sqrt{x^2+1+x}+\sqrt{x^2+1-x})
le signe de la dérivée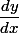 est difficile à étudier, par contre f est strictement croissante sur
est difficile à étudier, par contre f est strictement croissante sur
l'intervalle comme somme de deux fonctions strictement croissantes.
comme somme de deux fonctions strictement croissantes.
élever au carré une première fois, il vient:
=2\sqrt{(x^2+1)^2-x^2})
élever au carré une seconde fois, il vient:
}{4(1-y^2)})

le signe de la dérivée
l'intervalle
élever au carré une première fois, il vient:
élever au carré une seconde fois, il vient:
Re: Fiction reciproque
Bonjour
Je rajouterais, mais cela tombe sous le sens, que y est élément de [f(1/2);+inf[
Comme f(1/2) >2 cela permet de dire que 1-y² est non nul lors de la division par 4(1-y²)
Je rajouterais, mais cela tombe sous le sens, que y est élément de [f(1/2);+inf[
Comme f(1/2) >2 cela permet de dire que 1-y² est non nul lors de la division par 4(1-y²)
Re: Fiction reciproque
re,
soit le traceur de courbes https://www.mathe-fa.de/fr
(rentrer \sqrt{x^2+x+1} pour la racine.)
le graphe suggère que f est strictement croissante sur l'intervalle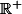
et l'image de cet intervalle est l'intervalle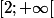
f est strictement décroissante sur l'intervalle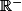
et l'image de cet intervalle est l'intervalle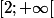
soit le traceur de courbes https://www.mathe-fa.de/fr
(rentrer \sqrt{x^2+x+1} pour la racine.)
le graphe suggère que f est strictement croissante sur l'intervalle
et l'image de cet intervalle est l'intervalle
f est strictement décroissante sur l'intervalle
et l'image de cet intervalle est l'intervalle
Re: Fiction reciproque
Salut,
A la main, c'est pas la mer à boire non plus :
>0\ \Leftrightarrow\ \dfrac{2x+1}{2\sqrt{x^2\!+\!x\!+\!1}}+\dfrac{2x-1}{2\sqrt{x^2\!-\!x\!+\!1}}>0)
\sqrt{x^2\!-\!x\!+\!1}>(1\!-\!2x)\sqrt{x^2\!+\!x\!+\!1})
qui, vu les signes des deux membres, est trivialement vrai pour x>1/2 et trivialement faux pour x<-1/2.
Et si x est entre -1/2 et 1/2 les deux membres sont positif et l'inéquation est équivalente à celle obtenue en les élevant au carré ;
(x^2\!-\!x\!+\!1)>(4x^2\!-\!4x\!+\!1)(x^2\!+\!x\!+\!1))
\!\times\!(-2x)+4x\!\times\!(2x^2\!+\!2)>0)

A la main, c'est pas la mer à boire non plus :
qui, vu les signes des deux membres, est trivialement vrai pour x>1/2 et trivialement faux pour x<-1/2.
Et si x est entre -1/2 et 1/2 les deux membres sont positif et l'inéquation est équivalente à celle obtenue en les élevant au carré ;
Modifié en dernier par Ben314 le 07 Nov 2021, 17:23, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Fiction reciproque
Ben314 a écrit:Salut,
A la main, c'est pas la mer à boire non plus :>0\ \Leftrightarrow\ \dfrac{2x+1}{2\sqrt{x^2\!+\!x\!+\!1}}+\dfrac{2x-1}{2\sqrt{x^2\!-\!x\!+\!1}}>0)
erratum: lire f'(x)>0 merci Ben.
Modifié en dernier par mathelot le 07 Nov 2021, 17:23, modifié 1 fois.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
