Bonjour,
Dans mon exercice il me demande de démontrer que: ((2)+i2)^8 est un nombre réel positif.
J'ai dis que Arg (((2)+i2)^8)=0 [2pi]
8Arg((2)+i2)=0+k*2pi
Après ça j'ai calculé l'argument où j'ai trouvé pi/4
Ensuite après avoir trouvé l'argument j'ai écris 8pi/4=k*2pi
Après je bloque je ne sais pas comment terminé...
Merci
Exercice nombres complexes
4 messages
- Page 1 sur 1
Re: exercice nombres complexes
Bonjour ;
^8 = (2(1 + i))^8 = 2^8(1+i)^8 .)
Il suffit de calculer^2) ;
; ^4) et enfin
et enfin ^8) , ce qui te permettra de conclure .
, ce qui te permettra de conclure .
Tu peux aussi procéder ainsi :
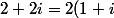 = 2\sqrt 2(\dfrac{\sqrt 2}{2} + i \dfrac{\sqrt 2}{2}) = 2\sqrt 2(cos(\dfrac{\pi}{4}) + i sin(\dfrac{\pi}{4})) = 2\sqrt 2 e^{i\dfrac{\pi}{4}} ,)
ceci te permettra aussi de conclure .
Il suffit de calculer
Tu peux aussi procéder ainsi :
ceci te permettra aussi de conclure .
Modifié en dernier par aymanemaysae le 05 Mar 2018, 14:36, modifié 1 fois.
Re: exercice nombres complexes
Ne pars pas de la conclusion, montre-le directement
je pense que c'est 8pi/4 dans " j'ai calculé l'argument où j'ai trouvé pi/4"
((2)+i2)^8 = (2*(1+i))^8 = (2racine(2).exp(i pi/4))^8
(une valeur possible de) son argument vaut bien 8*pi/4=2pi
qui vaut aussi 0 modulo 2pi
c'est bien un nombre réel
je pense que c'est 8pi/4 dans " j'ai calculé l'argument où j'ai trouvé pi/4"
((2)+i2)^8 = (2*(1+i))^8 = (2racine(2).exp(i pi/4))^8
(une valeur possible de) son argument vaut bien 8*pi/4=2pi
qui vaut aussi 0 modulo 2pi
c'est bien un nombre réel
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
