Exercice Nombres complexes

par **deadinsoul** » 19 Fév 2012, 23:29

Manny06 a écrit:attention au sens de l'inégalité
tu as divisé par ln(1/V2) qui est negatif donc l'inégalité change de sens
n>=8,64 et n entier donc n>=9

Ah oui c'est vrait que ln(x) est négatif entre 0 et 1 merci ^^.

je suis bloqué pour la 4a) je remplace z(n+1) pas (1+i)/2 et au final je trouve 1 et non i, a chaque fois :s

par **deadinsoul** » 19 Fév 2012, 23:44

Je tombe sur (-zn + izn)/(zn+izn), ma calculette me donne i comme résultat mais je ne voi pas comment continuer mon calcul.

par **deadinsoul** » 19 Fév 2012, 23:53

Manny06 a écrit:attention au sens de l'inégalité
tu as divisé par ln(1/V2) qui est negatif donc l'inégalité change de sens
n>=8,64 et n entier donc n>=9

(z(n+1)-zn)/z(n+1) = [(1+i)/2 * zn - zn] /[(1+i)/2 * zn]
=(zn + izn - 2zn)/(zn + izn)
=(zn(-1+i))/(zn(1+i))
=(-1+i)/(1+i)
=(-1+i)(1-i)
=-1 + i + i + 1 = 2i

toujours pas bon :s

par **Dinozzo13** » 20 Fév 2012, 00:14

Re-Salut !
Pour tout entier naturel n,

par **Dinozzo13** » 20 Fév 2012, 00:15

deadinsoul a écrit:(...)
=(-1+i)/(1+i)
=(-1+i)(1-i)
(...)

Ton problème est ici :

par **deadinsoul** » 20 Fév 2012, 00:33

Dinozzo13 a écrit:Ton problème est ici :

Ah mais je croi avoir trouvé mon erreur lorsqu'on multiplie par le conjugué on le laisse en bas, pour je le supprimais a chaque fois ! Merci beaucoup !!

par **globule rouge** » 20 Fév 2012, 00:46

Pour la 4)a), il te faut remarquer que l'on peut réécrire

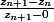
dont un argument représente la valeur principale de

qui vaut

par **deadinsoul** » 20 Fév 2012, 00:50

Dinozzo13 a écrit:Ton problème est ici :

On en déduit que les triangle OAnAn+1 est isocèle rectangle en An+1 ?

4b)ln = Uo * (q^(n+1) - 1) / (q - 1)
ln= 2 * [(1/V2)^(n+1) -1]/ (1/V2 - 1)

par **Dinozzo13** » 20 Fév 2012, 01:31

En effet, car d'après ce une formule sur les angles orientés

:+++:

par **deadinsoul** » 20 Fév 2012, 12:08

Dinozzo13 a écrit:En effet, car d'après ce une formule sur les angles orientés :+++:

Je suis toujours bloqué sur cette limite :/

par **globule rouge** » 20 Fév 2012, 12:27

deadinsoul a écrit:Je suis toujours bloqué sur cette limite :/

Bonjour !
Pour ce faire, il faut d'abord que tu calcules

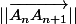
qui vaut :

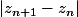
pour enfin trouver

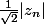
autrement dit,

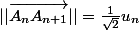
Tu n'as plus qu'à calculer

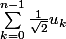
et en déduire

.
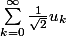
J'espère que tu as compris la méthode =)

par **Gnagna** » 18 Déc 2014, 17:32

J'ai le même exercice, le problème c'est que je n'ai pas encore appris a me servir de In :hum: Du coup je rame un peu :help:

par **capitaine nuggets** » 18 Déc 2014, 18:22

Salut !
Voir ici.

Exercice Nombres complexes

Qui est en ligne