événements élémentaires

[alexis6]

Bonsoir,

Voici trois questions sûrement très naïves en théorie des probabilités.

1) Une expérience consiste t-elle en l'explication d'un procédé ( par exemple, lancer un dé à six faces ) ou bien en l'explication d'un procédé et la donnée d'un critère permettant de définir un résultat? ( par exemple, lancer un dé à six faces et obtenir {1, 2, ... 6} )

2) Supposons que soit donnée l'explication d'un procédé, par exemple lancer un dé. Comment définir les événements élémentaires, et comment être sûrs qu'ils ne soient pas composés?

3) En théorie des probabilités, quelle est la nature mathématique d'une part de l'expérience, d'autre part de l'événement?

Merci d'avance

[Ben314]

Salut,
Les questions sont "un peu vagues", mais on peut tenter d'y répondre.
Forcément, ça sera pas trés "carré" et d'autres intervenant peuvent avoir des avis divergeant du mien...

1) Pour moi une "expérience", pour qu'on puisse la modéliser en math., c'est la donnée d'un "procédé" comme tu dit (on parle plutôt d'une "expérience aléatoire" mais on s'en fout) ET d'un "résultat" de l'expérience qu'on va observer, qui peut être numérique ou pas (couleur d'un truc...) et qui peut être de "dimension 1" (une seule valeur, par exemple la somme des dés) ou pas (on jette 4 dés et on s'intéresse au couple (min_obtenu,max_obtenu) )

2) Face à un problème concret, tu as systématiquement plusieurs façons de le "modéliser" mathématiquement et souvent tu as plusieurs modélisation dont les "évènements élémentaire" ne sont pas les mêmes.
Si on peut, c'est souvent mieux que les "évènement élémentaires" de la modélisation soient équiprobable vu que ça facilite les calculs (mais ce n'est évidement pas toujours possible et, même si c'est possible, il y a des fois où ce n'est pas le plus malin).
Souvent (mais pas toujours) on préfère qu'il n'y ait "pas trop" d'évènement élémentaires, mais s'ils ne sont pas équiprobables, il faut évidement s'assurer qu'on arrive relativement facilement à calculer la proba de chacun d'eux.
Enfin, bref, c'est assez régulièrement une partie un peu difficile de l'exercice de trouver la "bonne" modélisation.

3) Dans le cas fini (i.e. un nombre fini "d'évènements élémentaires" dans la modélisation), c'est pas trop compliqué le modèle mathématique : on a un ensemble (fini) contenant tout les "évènements élémentaires" et une fonction 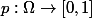qui à chaque "évènements élémentaires" associe sa probabilité avec comme seule hypothèse que la somme des pour tout les 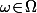vaut 1.
Dans le cas infini, c'est "vaguement plus ou moins pareil", mais... en beaucoup plus compliqué... (a mon avis pas mal hors de porté d'un Lycéen...)

[beagle]

Pour la 1) je pense que cela dépend où on lance les dés.
Si tu lances les dés dans la Seine, si tu les lances sur le prof de maths,
ben faut penser avant au résultat que cela va produire ...

[alexis6]

Merci pour cette réponse détaillée.

1) D'accord, donc l'expérience définit les événements élémentaires. Du coup, par exemple si mon expérience c'est " lancer un dé à six faces et regarder s'il tombe sur { 2, 4, 6 } ", je ne pourrais pas sur cette expérience associer de probabilité, car p( {2,4,6} ) = 1/2 différent de 1. Ai-je juste?

Par ailleurs, je lis dans un autre cours:
" Il n’est pas toujours facile de trouver un ensemble Ω permettant de modéliser une expérience aléatoire. Voici une règle pratique pour y arriver : les événements élémentaires sont ceux qui contiennent l’information maximale qu’il est possible d’obtenir de l’expérience. Par exemple si on jette un dé, l’événement A : « obtention d’un chiffre pair » n’est pas élémentaire. Il est composé des trois événements élémentaires 2, 4, 6 : A = {2,4,6}. Ici Ω = {1,2,3,4,5,6}. "

Etant donné que vous m'avez écrit que la définition d'une expérience équivalait à la définition d'un procédé et la donnée de résultats ( événements élémentaires ), dans ce cas là les événements élémentaires ne sont pas " ceux qui contiennent l'information maximale ", mais bien ceux que j'ai définis non?

2)
" Face à un problème concret, tu as systématiquement plusieurs façons de le "modéliser" mathématiquement "

J'ai deux questions:
Aura t-on les mêmes résultats selon la modélisation?

3) Ok

J'ai cherché sur internet la définition d'une expérience, et voici ce que j'ai obtenu:

- une expérience aléatoire est une expérience renouvelable (en théorie si ce n'est en pratique), et qui, renouvelée dans des conditions identiques – pour autant que l'observateur puisse s'en assurer – ne donne pas forcément le même résultat à chaque renouvellement
- une expérience aléatoire est une expérience dont on ne peut pas prévoir le résultat de façon certaine.
- une expérience aléatoire est une expérience dont l'issue (le résultat) dépend du hasard.

Et j'en ai beaucoup d'autres comme ça. Le problème est que toutes les phrases commence par " une expérience est une expérience "... ( tautologie ). Ces définitions ne donnent donc que le sens de aléatoire. Je n'ai vraiment rien eu en cherchant, comme si le concept d'expérience tombait sous le sens.

[Ben314]

1) D'accord, donc l'expérience définit les événements élémentaires. Du coup, par exemple si mon expérience c'est " lancer un dé à six faces et regarder s'il tombe sur { 2, 4, 6 } ", je ne pourrais pas sur cette expérience associer de probabilité, car p( {2,4,6} ) = 1/2 différent de 1. Ai-je juste?

A mon sens, non, ce n'est pas "juste" : ton expérience, c'est "lancer un dés à 6 face" et il faut que tes "évènements élémentaires" décrivent tout les résultats possibles de l'expérience en question.
Donc ce que à peu prés tout le monde ferait dans un cas pareil, c'est de prendre comme "évènement élémentaire" les 6 valeurs possibles du dés : et, comme fonction de probabilité pour tout en admettant que le dés est équilibré (i.e. que toutes les faces sont équiprobables). Et, vu l'énoncé, le "résultat étudié" serait de savoir si ou pas ( désigne un des éléments de donc un entier entre 1 et 6)
Pour te donner un exemple d'une autre modélisation, vu l'énoncé, on pourrait ne mettre que deux éléments dans , à savoir {2,4,6} et {1,3,5} ( serait donc un ensemble d'ensembles) avec une proba de 1/2 sur chacun d'eux et dans ce cas, le résultat étudié serait de savoir si ou pas ( désigne un des éléments de donc soit {2,4,6}, soit {1,3,5})

Par ailleurs, je lis dans un autre cours:
" Il n’est pas toujours facile de trouver un ensemble Ω permettant de modéliser une expérience aléatoire. Voici une règle pratique pour y arriver : les événements élémentaires sont ceux qui contiennent l’information maximale qu’il est possible d’obtenir de l’expérience. Par exemple si on jette un dé, l’événement A : « obtention d’un chiffre pair » n’est pas élémentaire. Il est composé des trois événements élémentaires 2, 4, 6 : A = {2,4,6}. Ici Ω = {1,2,3,4,5,6}. "

Je suis tout a fait d'accord sur "l'idée générale" du laïus en question, mais moyennement d'accord sur la façon de l'écrire sur le plan théorique : Une fois que tu as choisi ton espace , un "évènement élémentaire", c'est un élément de , mais avant d'avoir choisi , ce n'est pas clair, au niveau mathématique, ce que désigne le terme "évènement élémentaire" (voir l'exemple ci dessus où, dans la deuxième modélisation, le fait d'obtenir 2,4 ou 6 a été considéré comme "élémentaire"). Donc, pour moi, ce laïus donne un conseil concernant un choix en général judicieux pour le qui incite par exemple à choisir la modélisation 1 plutôt que la 2 dans l'exemple de départ. Mais c'est uniquement un bon conseil de prendre pour les évènement "les plus petits possible" qui viennent à l'esprit (qui assez souvent vont être équiprobables). Ce n'est pas une obligation.

Aura t-on les mêmes résultats selon la modélisation ?

Comme toujours en mathématique, le résultat ne dépend pas de la méthode employée pour faire les calculs donc on doit trouver la même chose quelque soit la modélisation.
Dans la pratique, il peut arriver qu'on trouve des résultats différent vu qu'assez souvent, l'énoncé est ambigüe (est-ce un tirage avec remise ou pas ?, les évènement "trucs" et "bidule" sont ils supposés indépendants ?, etc...) et comme il y a plusieurs interprétations possibles de l'énoncé il y a plusieurs résultats différents.
Par exemple, tu trouvera sur le net des tas de nombreux "paradoxes" de proba tous liés au fait que le même énoncé peut être interprété de différentes façons. Mais il faut bien comprendre que ça signifie uniquement que l'énoncé de départ est mal formulé.

Je n'ai vraiment rien eu en cherchant, comme si le concept d'expérience tombait sous le sens.

C'est effectivement comme ça qu'il faut le comprendre et c'est assez normal : la question posée n'est pas une question concernant uniquement les maths. (où il faudrait espérer avoir une répons "archi carrée"), mais une question de modélisation mathématique : qu'est ce qui, dans la vie "réelle" peut se modéliser à l'aide de l'outil probabilité des mathématiques ?
Comme la question parle de "la vie réelle", elle sort du strict cadre des mathématiques théoriques et pour donner une réponse, il faut utiliser le vocabulaire "de la vie réelle" qui est forcément pas super "carré carré".
Donc là, pour répondre a ta question, il faut ouvrir un dictionnaire (de Français et pas de Math) pour voir ce que veut dire "une expérience" et forcément, ça sera pas "archi carré" comme réponse.

[beagle]

Juste pour le dé 6 faces je n'observe que 2,4,6.
C'est tout à fait possible.
Par exemple je veux une proba de 1/5 et je n'ai qu'un dé 6 faces,
ben je vire une face la 4 par exemple.
Quand le dé tombe sur 4 je relance le dé, le 4 ne compte pas.
Les évènements observés seront les 1,2,3,5,6 qui seront en équiproba de 1/5.
tomber sur 4 n'est pas ici une information, ce n'est pas un évènement observé, c'est juste une particularité du protocole.Il n'appartient pas aux résultats observés.

Après si tu veux faire cela avec le 2,4,6
et virer le 1,3,5, tu peux faire idem,
mais aussi tu peux renuméroter les 1,3,5, avec tes 2,4,
1 est 4; 3 est 2 ; 5 est 6.

Pour moi l'expérience ben c'est chercher un truc.
Je cherche à montrer que ceci ou cela
et pour cela j'invente un protocole.
Ton expérience n'est plus une expérience
ton expérience est un protocole, te voilà bien avancé.
Faut dire que tu es toujours aussi carré carré dans tes recherches,
c'est marrant, c'est bien
mais des fois aussi faut se détendre, ne pas ètre hyper-rigide,
tout ne rentre pas dans des cases avec de belles étiquettes.
Mais bravo quand même dans l'ensemble!

PS: par exemple:
expérience expérimenter =
faire un essai, essayer pour voir, pour montrer, pour démontrer