Etude de fonction racine carré
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 07 Sep 2014, 11:24
par Maths-ForumR » 07 Sep 2014, 11:24
Bonjour je suis bloqué sur un exercice,
Soit f(x) = Racine (-x²+3x-2)
a) Trouver l'ensemble de définition.
b)Étudier les variation.
c) f est -elle dérivable aux borne de Df.
d)F est- elle bornée sur son ensemble de définition
e)Prouver que la droite A d'eq : [x=3/2] est axe de symétrie de Cf.
a) Df= ] -00;1[ U ] 2;+00[
b) f'(x)= -2x+3/ ((2 racine(-x²+3x-2))
c) Je pense que non car se sont des valeur interdite mais je ne suis pas sur
d) Je ne sais pas
e) Également
Merci d'avance
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 07 Sep 2014, 11:57
par Shew » 07 Sep 2014, 11:57
Maths-ForumR a écrit:Bonjour je suis bloqué sur un exercice,
Soit f(x) = Racine (-x²+3x-2)
a) Trouver l'ensemble de définition.
b)Étudier les variation.
c) f est -elle dérivable aux borne de Df.
d)F est- elle bornée sur son ensemble de définition
e)Prouver que la droite A d'eq : [x=3/2] est axe de symétrie de Cf.
a) Df= ] -00;1[ U ] 2;+00[
b) f'(x)= -2x+3/ ((2 racine(-x²+3x-2))
c) Je pense que non car se sont des valeur interdite mais je ne suis pas sur
d) Je ne sais pas
e) Également
Merci d'avance
Déjà partons de la base, quel est l'ensemble de definition de la fonction racine carré ?
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 07 Sep 2014, 12:19
par Maths-ForumR » 07 Sep 2014, 12:19
Df = [0;+00[
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 07 Sep 2014, 12:22
par Shew » 07 Sep 2014, 12:22
Maths-ForumR a écrit:Df = [0;+00[
Donc votre réponse a est fausse puisque l'intervalle est strict alors qu'il devrait être large
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 07 Sep 2014, 12:24
par Maths-ForumR » 07 Sep 2014, 12:24
Donc c'est ] -00;1] U [2;00[ ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 07 Sep 2014, 12:25
par Shew » 07 Sep 2014, 12:25
Maths-ForumR a écrit:Donc c'est ] -00;1] U [2;00[ ?
Oui c'est ça
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 07 Sep 2014, 12:26
par Maths-ForumR » 07 Sep 2014, 12:26
Merci et pour la b) ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 07 Sep 2014, 12:30
par Shew » 07 Sep 2014, 12:30
Maths-ForumR a écrit:Merci et pour la b) ?
On étudie le signe de
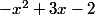
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 07 Sep 2014, 12:47
par Maths-ForumR » 07 Sep 2014, 12:47
-x² + 3x -2 est positif sur [1 ;2] et
-2x+3 est positif ] -00; 3/2 ]
Donc f'(x) est négatif sur ]-00 ; 1[
positif sur ] 1 ; 3/2 [ et ] 2 ; +00[
Donc f(x) décroissante sur ] -00 ; 1[
croissante sur 1 ; 3/2 [ et ] 2 ; +00[ ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 07 Sep 2014, 12:53
par Shew » 07 Sep 2014, 12:53
Maths-ForumR a écrit:-x² + 3x -2 est positif sur [1 ;2] et
-2x+3 est positif ] -00; 3/2 ]
Donc f'(x) est négatif sur ]-00 ; 1[
positif sur ] 1 ; 3/2 [ et ] 2 ; +00[
Donc f(x) décroissante sur ] -00 ; 1[
croissante sur 1 ; 3/2 [ et ] 2 ; +00[ ?
Autant pour moi c'est la variation et non le signe donc on ecrit la dérivé de la fonction
en prenant en compte le signe du trinome ce qui (pardon d'avance) remet en question le resultat de la question a (mauvaise interpretation de ma part encore pardon) .
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 07 Sep 2014, 13:29
par Maths-ForumR » 07 Sep 2014, 13:29
Donc le a est faux ?
Et ma derivé : f'(x)= -2x+3/ ((2 racine(-x²+3x-2)) c'est juste ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 07 Sep 2014, 13:32
par Shew » 07 Sep 2014, 13:32
Maths-ForumR a écrit:Donc le a est faux ?
Et ma derivé : f'(x)= -2x+3/ ((2 racine(-x²+3x-2)) c'est juste ?
Posez-vous la question suivante sachant que a = -1, quel est le signe du trinome en dehors de ses racines ? A l'interieur de ses racines ?
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 07 Sep 2014, 14:03
par Maths-ForumR » 07 Sep 2014, 14:03
Le signe du trinôme est du signe de a, donc négatif en dehors de ses racines
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 07 Sep 2014, 14:09
par Shew » 07 Sep 2014, 14:09
Maths-ForumR a écrit:Le signe du trinôme est du signe de a, donc négatif en dehors de ses racines
Donc f a pour ensemble de définition ?
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 07 Sep 2014, 14:25
par Maths-ForumR » 07 Sep 2014, 14:25
Comme solution j'ai trouvé x1 = 1 et x2 = 2 ce qui me ramène a ] -00;1] U [2;00[ ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 07 Sep 2014, 14:27
par Shew » 07 Sep 2014, 14:27
Maths-ForumR a écrit:Comme solution j'ai trouvé x1 = 1 et x2 = 2 ce qui me ramène a ] -00;1] U [2;00[ ?
Non puisque l'on a convenu que les valeurs d'une racine carré etaient positives ou nulles et que le trinome etait negatif en dehors de ses racines .
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 07 Sep 2014, 14:29
par Maths-ForumR » 07 Sep 2014, 14:29
Ah non pardon c'est plutôt Df= [1 ; 2] non ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 07 Sep 2014, 14:30
par Shew » 07 Sep 2014, 14:30
Maths-ForumR a écrit:Ah non pardon c'est plutôt Df= [1 ; 2] non ?
Voila c'est ce truc la :lol3:
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 07 Sep 2014, 14:32
par Maths-ForumR » 07 Sep 2014, 14:32
Merci ! donc pour la b) ma dérivé est elle juste ?
f'(x)= -2x+3/ ((2 racine(-x²+3x-2))
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 07 Sep 2014, 14:39
par Shew » 07 Sep 2014, 14:39
Maths-ForumR a écrit:Merci ! donc pour la b) ma dérivé est elle juste ?
f'(x)= -2x+3/ ((2 racine(-x²+3x-2))
La dérivée est bonne et etudiez -2x + 3 = 0 en vous souvenant que
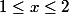
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
