Qu'est-ce qu'une forme convexe ?

[AlanShore]

Bonjour,

Je suis retraité et je me suis remis à l'étude des mathématiques.

En regardant la définition du carré : « Un carré est un quadrilatère convexe à quatre côtés de même longueur avec quatre angles droits ». Je me suis dis : "convexe" qu'est-ce que ça veut dire. Et j'ai cherché.

J'ai trouvé ça : https://fr.wikipedia.org/wiki/Polygone_convexe

- les angles du polygone sont tous inférieurs à 180 degrés, (compréhensible)
- tout segment joignant deux sommets du polygone est inclus dans la composante fermée bornée délimitée par le polygone. (incompréhensible)
- le polygone est toujours entièrement inclus dans un demi-plan dont la frontière porte un côté quelconque du polygone.(incompréhensible)

Quelqu'un peut-il m'éclairer ?

[GaBuZoMeu]

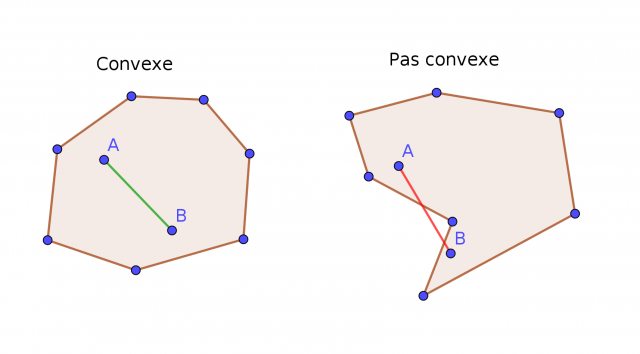
La définition de figure convexe : une figure F (partie du plan) est convexe quand, pour tous points A et B de F, le segment (rectiligne) qui joint A à B est tout entier contenu dans F.

[AlanShore]

La définition de figure convexe : une figure F (partie du plan) est convexe quand, pour tous points A et B de F, le segment (rectiligne) qui joint A à B est tout entier contenu dans F.

Excuses-moi, GaBuZoMeu, mais tu ne rends pas les choses plus simples Sans un dessin ces mots ne veulent rien dire pour moi. Je suis du genre qui comprend vite, mais qui nécessite une longue explication

J'ai repris un dessin de wikipédia :



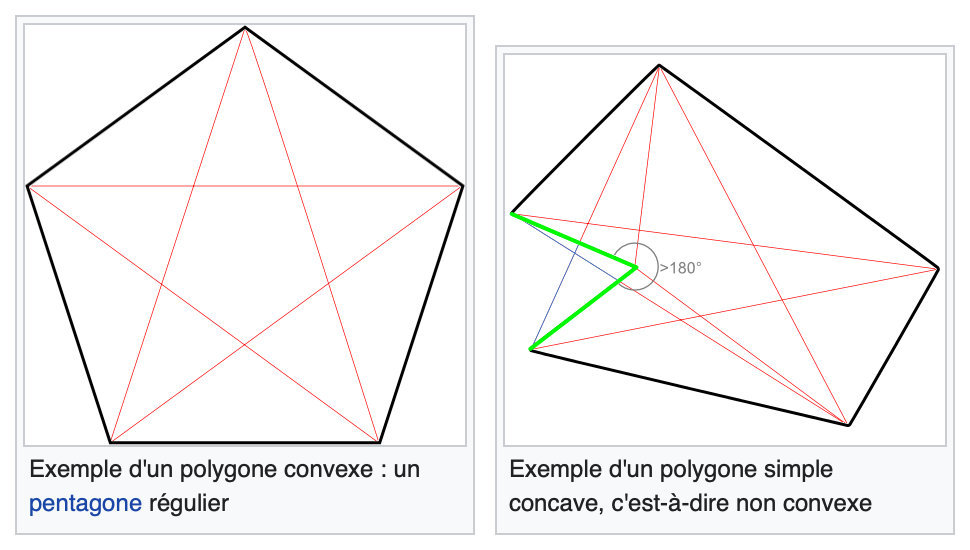
J'y ai rajouté des vecteurs reliant les sommets (en rouge).

- On voit que dans le polygone convexe tous ces vecteurs sont inscrits dans le polygone.
- Dans le polygone concave certaines parties (en bleu) de ces vecteurs échappent à l'univers du polygone. C'est comme si ils appartenaient à un autre univers (ou polygone) dont la partie visible sont les côtés en vert.

Partant de là, puis-je affirmer :

- Que la somme des angles d'un polygone convexe est toujours de 360°
- Que la somme des angles d'un polygone concave est toujours supérieure à 360° (puisqu'on a affaire à deux polygones (un visible et un invisible)).

Je crois que j'ai compris le point

tout segment joignant deux sommets du polygone est inclus dans la composante fermée bornée délimitée par le polygone.

Par contre, je n'ai toujours pas compris ce qu'est un demi-plan.

[AlexGagne10]

Wikipédia n'est pas un bon site pour apprendre. Pour faire simple, regarde ici.http://www.alloprof.qc.ca/BV/pages/m1196.aspx#convexes
Demi-plan
http://www.alloprof.qc.ca/bv/pages/m1317.aspx

PS: Un polygone n'est pas forcément égal à 360 °, mais chacun de ses angles est inférieur à 180°
Prenons l'exemple d'un heptagone régulier, la somme de ses angles est d'environ 900.2
La raison est qu'un heptagone possède 7 angles de 128.6°, donc 900.2°
Il est convexe, car TOUS ses angles sont inférieurs à 180° et cela peut importe la somme des angles

[AlexGagne10]

Voilà un heptagone.

[GaBuZoMeu]

AlanShore, il faut aussi apprendre à lire ce qui est écrit et à le comprendre.
Est-ce si difficile de comprendre la définition de "convexe" ?

une figure F (partie du plan) est convexe quand, pour tous points A et B de F, le segment (rectiligne) qui joint A à B est tout entier contenu dans F.