Bonjour,
Voila l'énoncé :
Soit (0; vecteur i, vecteur j) un repère de l'ensemble des points du plan.Soit m appartient au réel . On considère les droites:
Delta : y= -3x+1 et Dm : y (m-1/2)x+2m+3/5
Question 1. Pour quelle valeur de m les droites Delta et Dm sibt- elles parallèles
Question 2. Dans le cas où Delta et Dm ne sont pas parallèles donner, en fonction de m , les coordonnées du point d'intersection noté Gm.
Question 3. Existe-t-il un point A appartenant a Dm quelle que soit la valeur de M ?
Voila est ce que vous pouvez m'aider a juste démarer les questions .
Merci d'avance
Equation de droites avec un paramètre
9 messages
- Page 1 sur 1
Question 2. Dans le cas où Delta et Dm ne sont pas parallèles donner, en fonction de m , les coordonnées du point d'intersection noté Gm.
si 2 droites sont sécantes, les coordonnées du point commun vérifie l'équation des 2 droites
GM(xM;yM)
yM= -3xM+1
yM =(m-1/2)xM+2m+3/5
donc -3xM+1 =(m-1/2)xM+2m+3/5
si 2 droites sont sécantes, les coordonnées du point commun vérifie l'équation des 2 droites
GM(xM;yM)
yM= -3xM+1
yM =(m-1/2)xM+2m+3/5
donc -3xM+1 =(m-1/2)xM+2m+3/5
Le point d'intersection 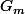 , de coordonnées
, de coordonnées ) est sur la droite
est sur la droite  ET sur la droite
ET sur la droite 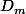
Donc ses coordonnées vérifient les équations des deux droites, en même temps.
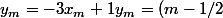x_m+2m+3/5)
Tu peux ainsi en déduire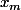
Et ensuite, tu en déduis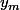 grâce à l'équation de l'une des deux droites.
grâce à l'équation de l'une des deux droites.
Mr.23
Donc ses coordonnées vérifient les équations des deux droites, en même temps.
Tu peux ainsi en déduire
Et ensuite, tu en déduis
Mr.23
« Je ne suis pas un numéro, je suis un homme libre ! »
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
