Equation différentiel 1er Ordre
24 messages
- Page 1 sur 2 - 1, 2
Equation différentiel 1er Ordre
Bonjour mesdame et monsieurs ,
Pourriez vous m'aider et détailler comment trouver la réponse cette équation différentiel s'il vous plait
Je met le lien ci dessous :
https://postimg.cc/56CF76fK
Pourriez vous m'aider et détailler comment trouver la réponse cette équation différentiel s'il vous plait
Je met le lien ci dessous :
https://postimg.cc/56CF76fK
Re: Equation différentiel 1er Ordre
bonjour,
l'équation différentielle est à variable séparée.
on a:
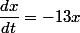
peux tu séparer les variables , en écrivant une équation de la forme f(x)dx=g(t)dt ?
où f et g sont deux fonctions continues
l'équation différentielle est à variable séparée.
on a:
peux tu séparer les variables , en écrivant une équation de la forme f(x)dx=g(t)dt ?
où f et g sont deux fonctions continues
Modifié en dernier par mathelot le 07 Jan 2021, 16:49, modifié 1 fois.
Re: Equation différentiel 1er Ordre
En effet je ne sais pas du tout equation diffectiell et on a pas encore commencer le cours c'est je beoins votre aide .
Re: Equation différentiel 1er Ordre
Liam20 a écrit:En effet je ne connais pas du tout les équations différentielles et l'on n'a pas encore commencé le cours, c'est pour cette raison que j'ai besoin de votre aide .
on sépare les variables:
on intègre en tenant compte des valeurs initiales:
(Ln est le logarithme népérien)
on prend l'exponentielle des deux membres:
Re: Equation différentiel 1er Ordre
Merci beaucoup pour corriger l'orthographe , Je suis très mauvais avec l'orthographe
Et merci aussi pour votre démonstration j'ai besoin juste la démonstation cette exo et pour le reste de exos je vais travailler tout seul.
Et merci aussi pour votre démonstration j'ai besoin juste la démonstation cette exo et pour le reste de exos je vais travailler tout seul.
Re: Equation différentiel 1er Ordre
Liam20 a écrit:Merci beaucoup pour corriger l'orthographe , Je suis très mauvais en orthographe
Et merci aussi pour votre démonstration, j'ai besoin juste de la démonstration de cet exo et pour les exercices restant, je vais travailler tout seul.
je pense qu'il y a une démonstration en appliquant le cours (Terminale STI?), mais mon calcul
n'utilise pas ce cours^^.
Est ce que tu connais ce que l'on appelle le calcul intégral et les primitives ?
Re: Equation différentiel 1er Ordre
Le calcul intégral et les primitives je connais un peu mais je vais essayer regarder sur youtube pour comprendre mieux.
Re: Equation différentiel 1er Ordre
Liam20 a écrit:Le calcul intégral et les primitives je connais un peu mais je vais essayer de regarder sur youtube pour mieux comprendre.
oui, tu as raison.
n'hésite pas à poser d'autres questions si besoin.
Re: Equation différentiel 1er Ordre
mathelot a écrit:
Bonjour madame pouvez vous faire démonstration cette exercice s'il vous plait ça fait depuis 1 jours j'arrive pas à trouver la solution , en fait ce sont les Equ. diffé compliquer je ne comprends pas , et mon prof a mis ces exos sur le site wims pour travailler mais je suis bloqué , vous pouvez voir la photo ci dessous :
1)
https://i.postimg.cc/qRP1BG1w/Capture8.jpg
2)
https://i.postimg.cc/SRcDnz5h/Capture9.jpg
Re: Equation différentiel 1er Ordre
bonjour,
on cherche une solution particulière) sous la forme
sous la forme 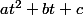
où a,b,c sont des réels.
on pose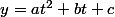 , on calcule
, on calcule 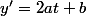 , on remplace
, on remplace  et
et 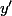 dans l'équation .
dans l'équation .
ça donne l'égalité de deux polynômes. Leur coefficients sont égaux.
on en déduit un système vérifié par a , b et c.
question 2
L'équation homogène est 2y'+5y=0
on cherche une solution particulière
où a,b,c sont des réels.
on pose
ça donne l'égalité de deux polynômes. Leur coefficients sont égaux.
on en déduit un système vérifié par a , b et c.
question 2
L'équation homogène est 2y'+5y=0
Re: Equation différentiel 1er Ordre
[quote="mathelot"][/quote]
Bonjour madame j'ai réussi et j'ai compris maintenant comment trouver Equ. diffé mais juste le dernière partie pour trouver y(0) = 3 comme l'exemple photo ci dessous j'ai pas compris comment calculer.
https://postimg.cc/S2swD4R6
Pouvez vous m'expliquer s'il vous plait.
Bonjour madame j'ai réussi et j'ai compris maintenant comment trouver Equ. diffé mais juste le dernière partie pour trouver y(0) = 3 comme l'exemple photo ci dessous j'ai pas compris comment calculer.
https://postimg.cc/S2swD4R6
Pouvez vous m'expliquer s'il vous plait.
Re: Equation différentiel 1er Ordre
bonjour,
la forme générale des solutions est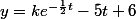
on cherche la solution vérifiant f(0)=3
d'où en remplaçant t par 0, il vient;
k+6=3
k=-3
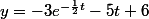
la forme générale des solutions est
on cherche la solution vérifiant f(0)=3
d'où en remplaçant t par 0, il vient;
k+6=3
k=-3
Re: Equation différentiel 1er Ordre
vous remplacez dans quelle partie K+6=3 comment vous avez trouver k+6 j'ai pas compris vous pouvez un peu détailler s'il vous plait
Re: Equation différentiel 1er Ordre
mathelot a écrit:la forme générale des solutions est
on cherche la solution vérifiant f(0)=3
d'où en remplaçant t par 0, il vient;
k+6=3
k=-3
Re: Equation différentiel 1er Ordre
Bonjour madame j'ai autres Equation .Diff , en fait j'ai appliqué comme la photo précédent mais ça ne marche pas parce que il y a (t) devant y donc je suis bloqué pouvez vous démonster s'il vous plait
L'objectif est de trouver les solutions de l'équation différentielle (E) sur R :
(E) y'−ty=−2t
1- Trouver une solution particulière constante de l'équation différentielle (E) :
f(t) : ????
L'objectif est de trouver les solutions de l'équation différentielle (E) sur R :
(E) y'−ty=−2t
1- Trouver une solution particulière constante de l'équation différentielle (E) :
f(t) : ????
Re: Equation différentiel 1er Ordre
Bonsoir,
Une solution particulière est toujours de la forme y = f(t) de sorte que si on remplace y et ses dérivées dans le premier membre de l'équation différentielle, on retrouve après simplification le second membre.
Ici, l'énoncé indique que cette solution est constante donc y est un réel ce qui implique y' = 0
Il reste donc à trouver ce réel de sorte à ce que -ty = -2t
Une solution particulière est toujours de la forme y = f(t) de sorte que si on remplace y et ses dérivées dans le premier membre de l'équation différentielle, on retrouve après simplification le second membre.
Ici, l'énoncé indique que cette solution est constante donc y est un réel ce qui implique y' = 0
Il reste donc à trouver ce réel de sorte à ce que -ty = -2t
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
