Bonjour, j'espère que vous allez bien !
Il y a une question à laquelle je reste bloquée...
Nous avons un plan π d'équation : -4x + 5y - z = 3. Nous avons également une droite D d'équation : (x,y,z) = (7,-1,2) + t(12,-6,-2). La question est la suivante : Trouvez l'équation d'une droite entièrement dans π qui soit perpendiculaire à la droite D au point (40/3, -25/6, 17/8).
Merci de m'aider !
Équation dans R3
10 messages
- Page 1 sur 1
Re: Équation dans R3
Bonjour,
Il y a un problème d'énoncé, le point indiqué n'appartient pas au plan, il suffit de remarquer le signe des coordonnées :
+\Big(5\times \dfrac{-25}{6}\Big)-\Big(\dfrac{17}{8}\Big)<0 \text{ donc } \neq 3)
Le point n'appartient pas non plus à la droite : en effet, en abscisse, si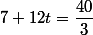 alors
alors 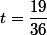 mais alors en côte on a
mais alors en côte on a 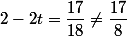 (mais en remplaçant 8 par 18, le point n'est quand même pas dans le plan).
(mais en remplaçant 8 par 18, le point n'est quand même pas dans le plan).
Sinon, après correction de l'énoncé : la droite recherchée sera l'intersection du plan avec le plan perpendiculaire à
avec le plan perpendiculaire à  et passant par le point indiqué. En effet, toute droite de ce second plan est orthogonale à
et passant par le point indiqué. En effet, toute droite de ce second plan est orthogonale à  , donc perpendiculaire à
, donc perpendiculaire à  si elles sont sécantes. Il n'y a donc qu'à trouver l'équation cartésienne de ce plan en utilisant le vecteur normal qui dirige la droite
si elles sont sécantes. Il n'y a donc qu'à trouver l'équation cartésienne de ce plan en utilisant le vecteur normal qui dirige la droite  et le système formé des équations cartésiennes des deux plans donne l'équation cartésienne de la droite.
et le système formé des équations cartésiennes des deux plans donne l'équation cartésienne de la droite.
Il y a un problème d'énoncé, le point indiqué n'appartient pas au plan, il suffit de remarquer le signe des coordonnées :
Le point n'appartient pas non plus à la droite : en effet, en abscisse, si
Sinon, après correction de l'énoncé : la droite recherchée sera l'intersection du plan
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Équation dans R3
Bonjour
En effet il y a une erreur.
Le point dont on donne les coordonnées doit être dans et sur(D).
et sur(D).
Si on cherche l'intersection du plan et de la droite (D) on trouve le point I(1,2,3).
et de la droite (D) on trouve le point I(1,2,3).
On pourrait donc corriger l'énoncé en prenant ces coordonnées.
En effet il y a une erreur.
Le point dont on donne les coordonnées doit être dans
Si on cherche l'intersection du plan
On pourrait donc corriger l'énoncé en prenant ces coordonnées.
Re: Équation dans R3
Merci à vous deux pour votre réponse !
Je vous montre l'énoncé directement :

Grâce aux points A, B et C, j'ai déterminé l'équation normale du plan π -4x + 5y - z = 3. Ensuite, j'ai réécris l'équation D sous cette forme : (x,y,z) = (7,-1,2) + t(12,-6,-2). Ensuite, j'ai substitué x, y et z dans l'équation de π par leur valeur (7+12t, -1-6t et 2-2t respectivement). Finalement, j'ai trouvé t = 19/36 et j'ai pu calculer le point d'intersection (40/3, -25/6, 17/8).
J'ai revérifié mes calculs et je ne vois pas d'erreur !!!
Je vous montre l'énoncé directement :
Grâce aux points A, B et C, j'ai déterminé l'équation normale du plan π -4x + 5y - z = 3. Ensuite, j'ai réécris l'équation D sous cette forme : (x,y,z) = (7,-1,2) + t(12,-6,-2). Ensuite, j'ai substitué x, y et z dans l'équation de π par leur valeur (7+12t, -1-6t et 2-2t respectivement). Finalement, j'ai trouvé t = 19/36 et j'ai pu calculer le point d'intersection (40/3, -25/6, 17/8).
J'ai revérifié mes calculs et je ne vois pas d'erreur !!!
Re: Équation dans R3
écris un peu le développement qui conduit au calcul de t car t est faux
tu devrais trouver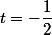
tu devrais trouver
Re: Équation dans R3
Pisigma a écrit:écris un peu le développement qui conduit au calcul de t car t est faux
tu devrais trouver
Bien sûr, voici ma démarche :
Re: Équation dans R3
revois la 3e ligne après "En substituant, on obtient:" et tu verras où tu t'es trompé(e)
Re: Équation dans R3
Pisigma a écrit:revois la 3e ligne après "En substituant, on obtient:" et tu verras où tu t'es trompé(e)
Ahhh oui merci je viens de voir mon erreur...
Maintenant que j'ai trouvé le point d'intersection (1,2,3), j'ai réussi à trouver la réponse à la question initiale. Voici ce que j'ai trouvé : (x,y,z) = (-1/3, 1/3, 0) + t(4,5,9)
(Pour ce faire j'ai considéré le vecteur directeur de la droite D comme le vecteur normal au plan recherché, j'ai calculé avec le point (1,2,3) pour trouver l'équation du plan normal à D : 12x-6y-2x = -6. Ensuite j'ai calculé le produit vectoriel des deux vecteurs normaux (-4,5,-1) et (12,-6,-2) et j'ai trouvé -4(4,5,9). Ensuite, pour trouver un point de la droite d'intersection, j'a posé z = 0 dans les deux équations des deux plans, j'ai trouvé le point (-1/3, 1/3, 0). Voilà !)
Re: Équation dans R3
Bonjour,
On a le plan d'équation : 4x - 5y + z + 3 = 0 (1)
Des relations du point a de l'énoncé, on tire :
y = 5/2 - x/2
et
z = -x/6 + 19/6
On remet ces résultats dans (1) --> 4x - 5(5/2 - x/2) - x/6 + 19/6 + 3 = 0
24x - 75 + 15x - x + 19 + 18 = 0
38x = 38
x = 1
y = 5/2 - 1/2 = 2
z = -1/6 + 19/6 = 3
P(1;2;3)
*********
vecteur directeur de la droite cherchée : (a ; b ; c)
12a - 6b - 2c = 0
6a - 3b - c = 0
On choisit par exemple a = 1 --> 3b + c = 6 ; c = 6 - 3b
Eq paramétriques de la droite cherchée :
x = 1 + t
y = 2 + b.t
z = 3 + (6 - 3b).t
Elle doit être dans le plan Pi
Donc le point (avec t = 1 par exemple) Q(2 ; 2+b ; 9 - 3b) doit appartenir à Pi.
4x - 5y + z + 3 = 0
8 - 5.(2+b) + 9 - 3b + 3 = 0
10-8b=0
b = 5/4
Eq paramétriques de la droite cherchée :
x = 1 + t
y = 2 + (5/4).t
z = 3 + (9/4).t
******
Résultats équivalent à ta réponse : (x,y,z) = (-1/3, 1/3, 0) + t(4,5,9)

On a le plan d'équation : 4x - 5y + z + 3 = 0 (1)
Des relations du point a de l'énoncé, on tire :
y = 5/2 - x/2
et
z = -x/6 + 19/6
On remet ces résultats dans (1) --> 4x - 5(5/2 - x/2) - x/6 + 19/6 + 3 = 0
24x - 75 + 15x - x + 19 + 18 = 0
38x = 38
x = 1
y = 5/2 - 1/2 = 2
z = -1/6 + 19/6 = 3
P(1;2;3)
*********
vecteur directeur de la droite cherchée : (a ; b ; c)
12a - 6b - 2c = 0
6a - 3b - c = 0
On choisit par exemple a = 1 --> 3b + c = 6 ; c = 6 - 3b
Eq paramétriques de la droite cherchée :
x = 1 + t
y = 2 + b.t
z = 3 + (6 - 3b).t
Elle doit être dans le plan Pi
Donc le point (avec t = 1 par exemple) Q(2 ; 2+b ; 9 - 3b) doit appartenir à Pi.
4x - 5y + z + 3 = 0
8 - 5.(2+b) + 9 - 3b + 3 = 0
10-8b=0
b = 5/4
Eq paramétriques de la droite cherchée :
x = 1 + t
y = 2 + (5/4).t
z = 3 + (9/4).t
******
Résultats équivalent à ta réponse : (x,y,z) = (-1/3, 1/3, 0) + t(4,5,9)
Re: Équation dans R3
Black Jack a écrit:Bonjour,
On a le plan d'équation : 4x - 5y + z + 3 = 0 (1)
Des relations du point a de l'énoncé, on tire :
y = 5/2 - x/2
et
z = -x/6 + 19/6
On remet ces résultats dans (1) --> 4x - 5(5/2 - x/2) - x/6 + 19/6 + 3 = 0
24x - 75 + 15x - x + 19 + 18 = 0
38x = 38
x = 1
y = 5/2 - 1/2 = 2
z = -1/6 + 19/6 = 3
P(1;2;3)
*********
vecteur directeur de la droite cherchée : (a ; b ; c)
12a - 6b - 2c = 0
6a - 3b - c = 0
On choisit par exemple a = 1 --> 3b + c = 6 ; c = 6 - 3b
Eq paramétriques de la droite cherchée :
x = 1 + t
y = 2 + b.t
z = 3 + (6 - 3b).t
Elle doit être dans le plan Pi
Donc le point (avec t = 1 par exemple) Q(2 ; 2+b ; 9 - 3b) doit appartenir à Pi.
4x - 5y + z + 3 = 0
8 - 5.(2+b) + 9 - 3b + 3 = 0
10-8b=0
b = 5/4
Eq paramétriques de la droite cherchée :
x = 1 + t
y = 2 + (5/4).t
z = 3 + (9/4).t
******
Résultats équivalent à ta réponse : (x,y,z) = (-1/3, 1/3, 0) + t(4,5,9)
Merciii !!!
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
