Dm à Rendre dans Trois Jours sur les Complexes dans le plan.
50 messages
- Page 3 sur 3 - 1, 2, 3
par SlImF 19 » 27 Jan 2015, 14:46
c)
E={M(z) , aff(M') est réel}
z' est réel si et seulement si z' =0 ou z' # 0 et Arg(z')=0(\pi)
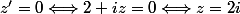
Si z'# 0
= arg(\frac{2+i z}{z-3i})=0(\Pi)=arg(\frac{(i \times (-2i+z)}{z-3i})=0(\Pi))
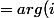+arg(\frac{z-2i}{z-3i})=O(\Pi))
= (\Pi/2)(\Pi))
= (\vec{DC},\vec{AB})(2pi))
 et H d'affixe (3i) \Longleftrightarrow (\vec{MH},\vec{MG})=\Pi/2(\Pi))
L'ensemble recherché est le cercle de diamètre [GH] privé de H
E={M(z) , aff(M') est réel}
z' est réel si et seulement si z' =0 ou z' # 0 et Arg(z')=0(\pi)
Si z'# 0
L'ensemble recherché est le cercle de diamètre [GH] privé de H
par SlImF 19 » 27 Jan 2015, 15:07
d)
F={M(z) , aff(M') est imaginaire pur}
z' est imaginaire pur si et seulement si z' =0 ou z' # 0 et=\Pi/2(\Pi))
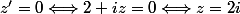
Si z'# 0
= arg(\frac{2+i z}{z-3i})=arg(\frac{(i \times (-2i+z)}{z-3i})=\Pi/2(\Pi))
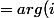+arg(\frac{z-2i}{z-3i})=\Pi/2(\Pi))
= -\Pi/2+\Pi/2(\Pi)=0(\Pi))
 et H d'affixe (3i) \Longleftrightarrow (\vec{MH},\vec{MG})=0(\Pi))
L'ensemble recherché est la droite (GH) privé de H
F={M(z) , aff(M') est imaginaire pur}
z' est imaginaire pur si et seulement si z' =0 ou z' # 0 et
Si z'# 0
L'ensemble recherché est la droite (GH) privé de H
par SlImF 19 » 27 Jan 2015, 15:25
d)
G={M(z) , aff(M') est telle que |z'|=1 }
}{z-3i}|=|i||\frac{z-2i}{z-3i}|=1)
|i|=1
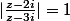
 et H d'affixe (3i) \Longleftrightarrow \frac{MK}{MH}=1)
L'ensemble recherché est le médiatrice de [KH]
G={M(z) , aff(M') est telle que |z'|=1 }
|i|=1
L'ensemble recherché est le médiatrice de [KH]
50 messages
- Page 3 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :