équation avec paramètre
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 04 Aoû 2009, 10:13
par Dinozzo13 » 04 Aoû 2009, 10:13
Bonjour, dans un premier temps, on me demande de déterminer suivant les valeurs de m le nombre de solutions de l'équation :
x^2-2mx+1=0)
, mais je me suis perdu, pourriez-vous m'aider ?
J'ai d'ores et déjà mis que si
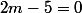
,
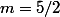
,
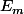
est du 1er degré donc on résous
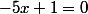
, d'où
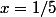
.
Si
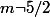
,
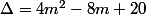
, mais après je ne sais pas quoi faire :triste:


-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 04 Aoû 2009, 10:42
par Ericovitchi » 04 Aoû 2009, 10:42
Et bien tu as calculé Delta, c'est bien.
On te demande de discuter le nombre de solutions suivant m.
Il faut se rappeler son cours. Si Delta positif : 2 solutions
Delta = 0 : 1 solution
Delta négatif : pas de solution
Donc il te faut étudier le signe de Delta ; Donc le signe de ce polynôme du second degré en m.
Sais tu étudier le signe d'un polynôme du second degré ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 04 Aoû 2009, 11:47
par Dinozzo13 » 04 Aoû 2009, 11:47
Ericovitchi a écrit:Et bien tu as calculé Delta, c'est bien.
On te demande de discuter le nombre de solutions suivant m.
Il faut se rappeler son cours. Si Delta positif : 2 solutions
Delta = 0 : 1 solution
Delta négatif : pas de solution
Donc il te faut étudier le signe de Delta ; Donc le signe de ce polynôme du second degré en m.
Sais tu étudier le signe d'un polynôme du second degré ?
oui, j'étais déjà parvenu à cette conclusion, mais je trouve ça bizarre de calculer un discriminant de discriminant :doh: .
-
johnjohnjohn
- Membre Rationnel
- Messages: 843
- Enregistré le: 24 Oct 2006, 11:00
-
 par johnjohnjohn » 04 Aoû 2009, 12:25
par johnjohnjohn » 04 Aoû 2009, 12:25
Dinozzo13 a écrit:oui, j'étais déjà parvenu à cette conclusion, mais je trouve ça bizarre de calculer un discriminant de discriminant :doh: .
ça te permettra d'étudier le signe de Delta justement ( en fonction des valeurs de m )
-
Black Jack
 par Black Jack » 04 Aoû 2009, 13:04
par Black Jack » 04 Aoû 2009, 13:04
4m²-8m+20
= (2m-2)² + 16
Alors quel est le signe de 4m²-8m+20 ?
...
:zen:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 04 Aoû 2009, 16:20
par Dinozzo13 » 04 Aoû 2009, 16:20

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 04 Aoû 2009, 16:38
par Ericovitchi » 04 Aoû 2009, 16:38
Oui, mais conclus bien, on s'en fiche des valeurs. la question était de discuter le nombre de racines. Comme le discriminant est toujours positif tu en déduis qu'il y a toujours 2 solutions sauf pour m=5/2 où il y en a qu'une.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 04 Aoû 2009, 16:42
par Dinozzo13 » 04 Aoû 2009, 16:42
Ok :ptdr: .
ensuite on me demande si on peut trouver une valeur de m pour que :
(2m-5)x²-2mx+1>0 pour tout x de IR .
Là je ne sais pas comment faire :doh:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 04 Aoû 2009, 16:47
par girdav » 04 Aoû 2009, 16:47
Bonjour.
Le discriminant étant toujours positif, on a que le trinôme est du signe du coefficient devant le terme de degré

. Donc il reste à étudier le signe de
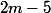
.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 04 Aoû 2009, 16:54
par Zweig » 04 Aoû 2009, 16:54
Non girdav. Le trinôme est du signe du coefficient du monôme de plus haut degré lorsque
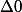
, alors le signe du trinôme est du signe de -

(coefficient du monôme de plus haut degré) lorsque
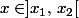
, du signe de

lorsque
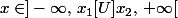
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 04 Aoû 2009, 17:35
par girdav » 04 Aoû 2009, 17:35
Oups exact.
Dans ce cas il n'y a pas de valeurs

qui vérifie la propriété.
-
Black Jack
 par Black Jack » 04 Aoû 2009, 17:44
par Black Jack » 04 Aoû 2009, 17:44
Dinozzo13 a écrit:Ok :ptdr: .
ensuite on me demande si on peut trouver une valeur de m pour que :
(2m-5)x²-2mx+1>0 pour tout x de IR .
Là je ne sais pas comment faire :doh:
A partir du moment où tu as démontré que, quel que soit m, il y a toujours 1 ou 2 solutions réelles à (2m-5)x²-2mx+1 = 0
La réponse à ta seconde question n'est-elle pas évidente ?
:zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités