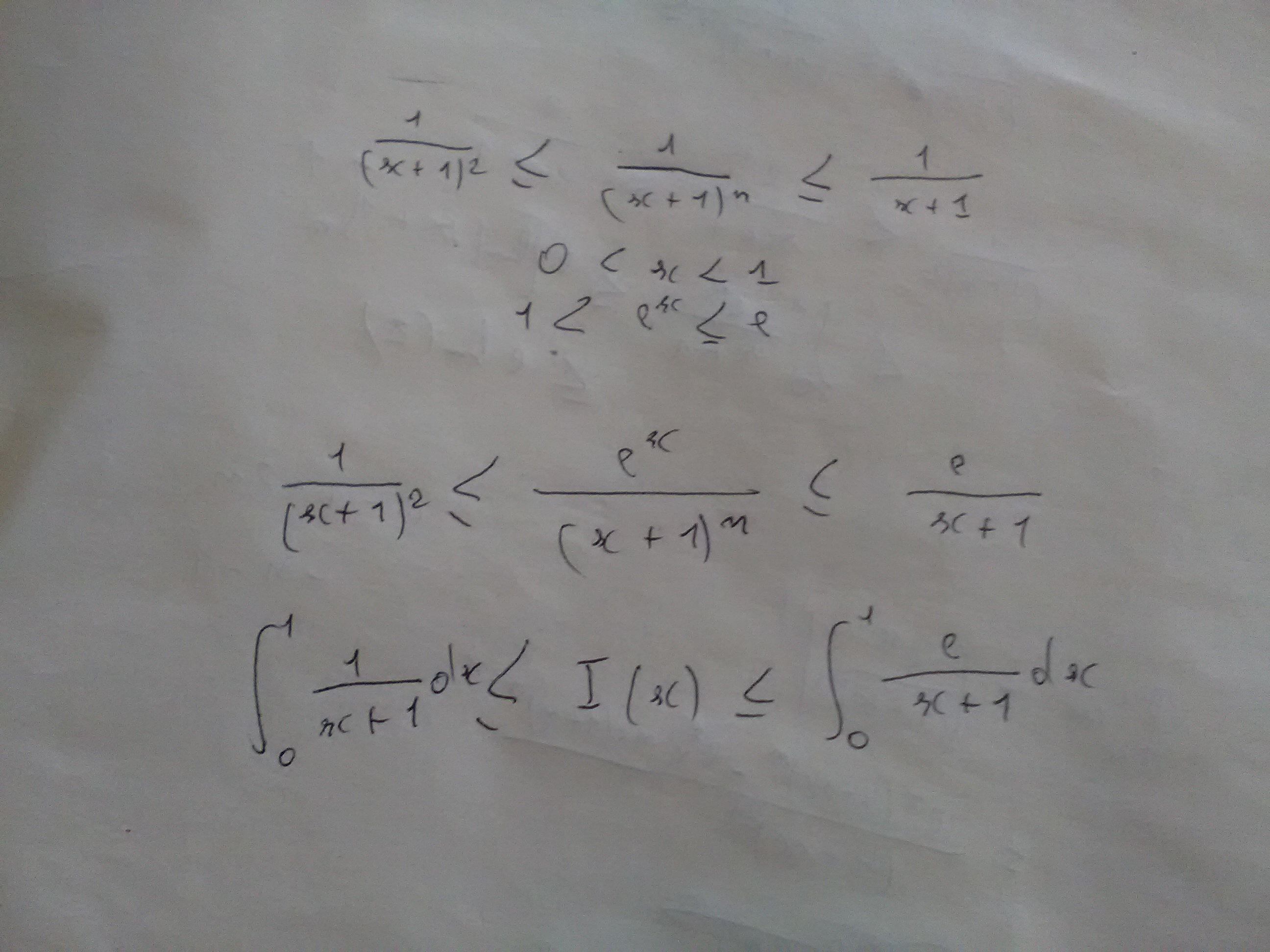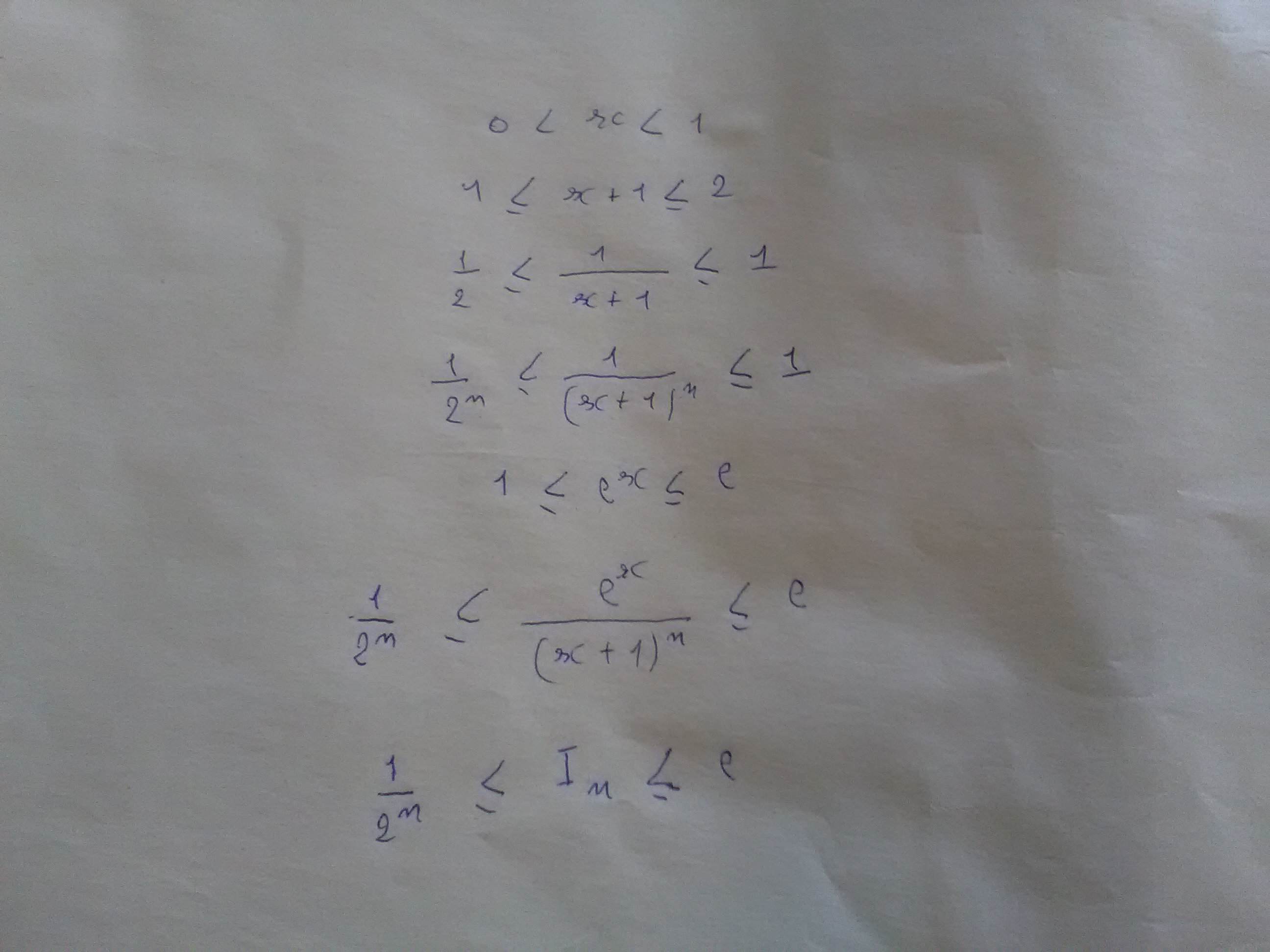Encadrement suite définie par integrale
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Kklpt87
- Messages: 4
- Enregistré le: 19 Déc 2019, 14:57
-
 par Kklpt87 » 21 Fév 2020, 16:01
par Kklpt87 » 21 Fév 2020, 16:01
Bonjour
J essaye en vain de prouver l encadrement suivant c'est la question 2 de l exercice 3
Je vous remercie d'avance.

-
GaBuZoMeu
- Habitué(e)
- Messages: 6142
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 21 Fév 2020, 16:26
par GaBuZoMeu » 21 Fév 2020, 16:26
Vu que dans tes inégalités, la différence entre ce qu'il y a à gauche et ce qu'il y a à droite c'est qu'on passe de 1 à

, que la fonction qu'on intègre est

fois quelque chose, et qu'on prend l'intégrale entre 0 et 1 ...
Tu vois où je veux en venir ?
-
Kklpt87
- Messages: 4
- Enregistré le: 19 Déc 2019, 14:57
-
 par Kklpt87 » 21 Fév 2020, 16:43
par Kklpt87 » 21 Fév 2020, 16:43
Je crois comprendre où tu veux en venir mais je reste toujours bloqué à ce stade
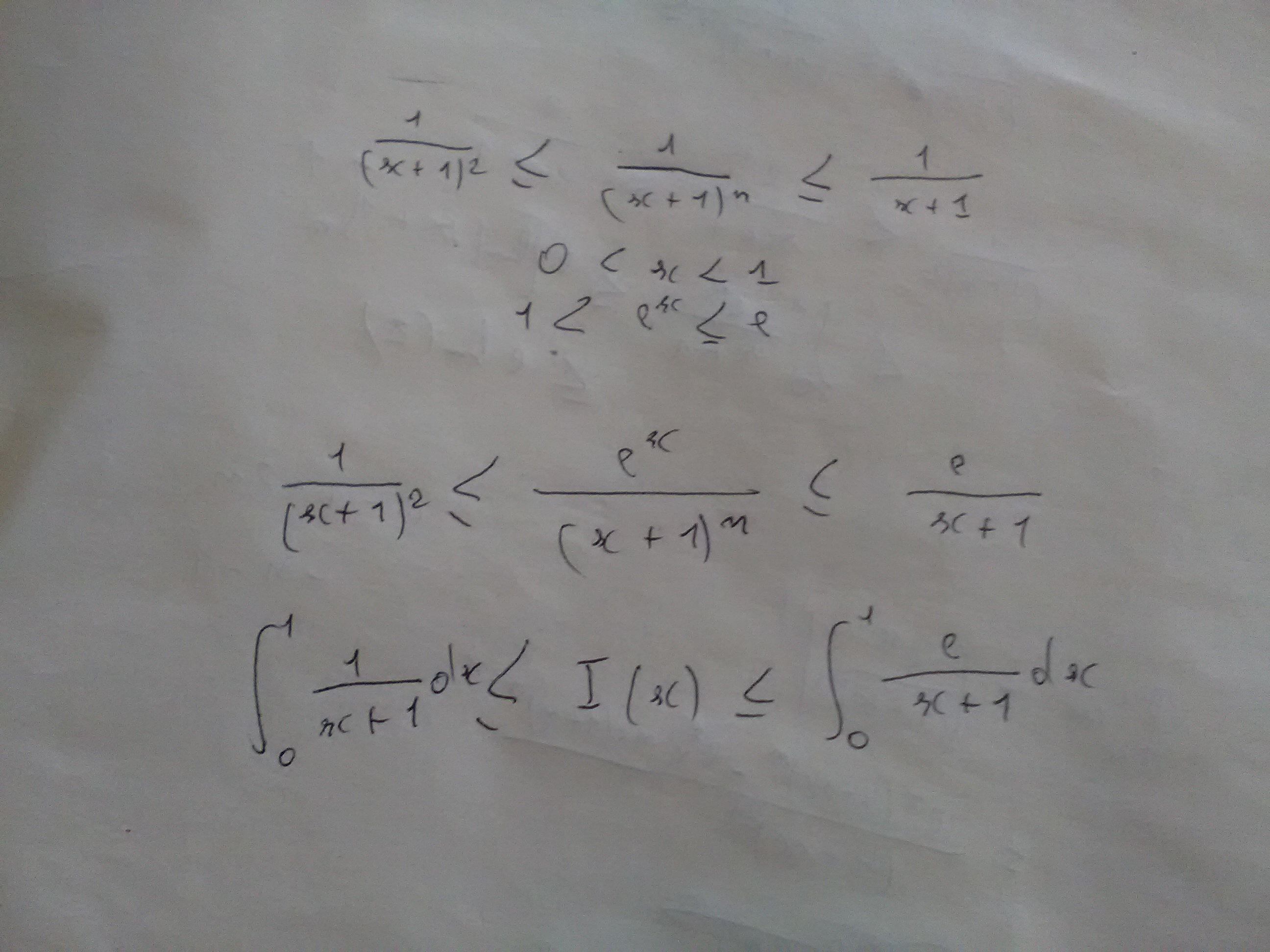
-
GaBuZoMeu
- Habitué(e)
- Messages: 6142
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 21 Fév 2020, 16:58
par GaBuZoMeu » 21 Fév 2020, 16:58
Ta première ligne, c'est n'importe quoi !
Tu as remarqué que les bornes de l'encadrement dépendent de

? Ce n'est donc pas une bonne idée de chercher à se débarrasser du

, et c'est une très mauvaise idée de le faire à ta façon, complètement erronée.
-
Kklpt87
- Messages: 4
- Enregistré le: 19 Déc 2019, 14:57
-
 par Kklpt87 » 21 Fév 2020, 17:09
par Kklpt87 » 21 Fév 2020, 17:09
Oui j avoue que c est pas malin d enlever le n , par contre en le gardant voici ce que j obtient
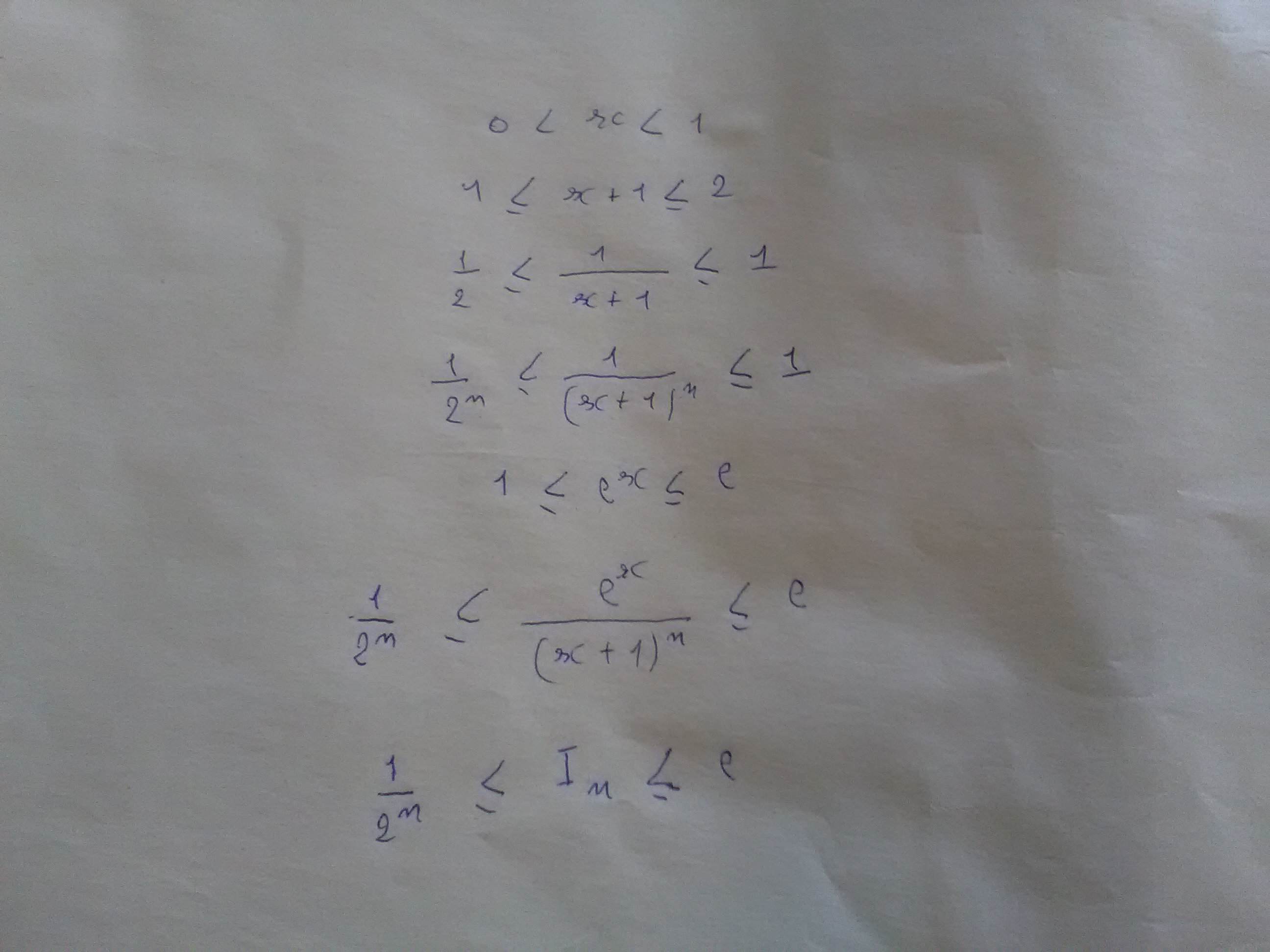
-
GaBuZoMeu
- Habitué(e)
- Messages: 6142
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 21 Fév 2020, 17:16
par GaBuZoMeu » 21 Fév 2020, 17:16
C'est déjà mieux. Mais ce n'est pas encore ça.
Tu devrais voir que si tu veux garder le rapport

entre minorant et majorant, c'est juste

qu'il convient d'encadrer (minorer/majorer) !
-
Kklpt87
- Messages: 4
- Enregistré le: 19 Déc 2019, 14:57
-
 par Kklpt87 » 21 Fév 2020, 17:34
par Kklpt87 » 21 Fév 2020, 17:34
Je crois que c est bon merci infiniment !
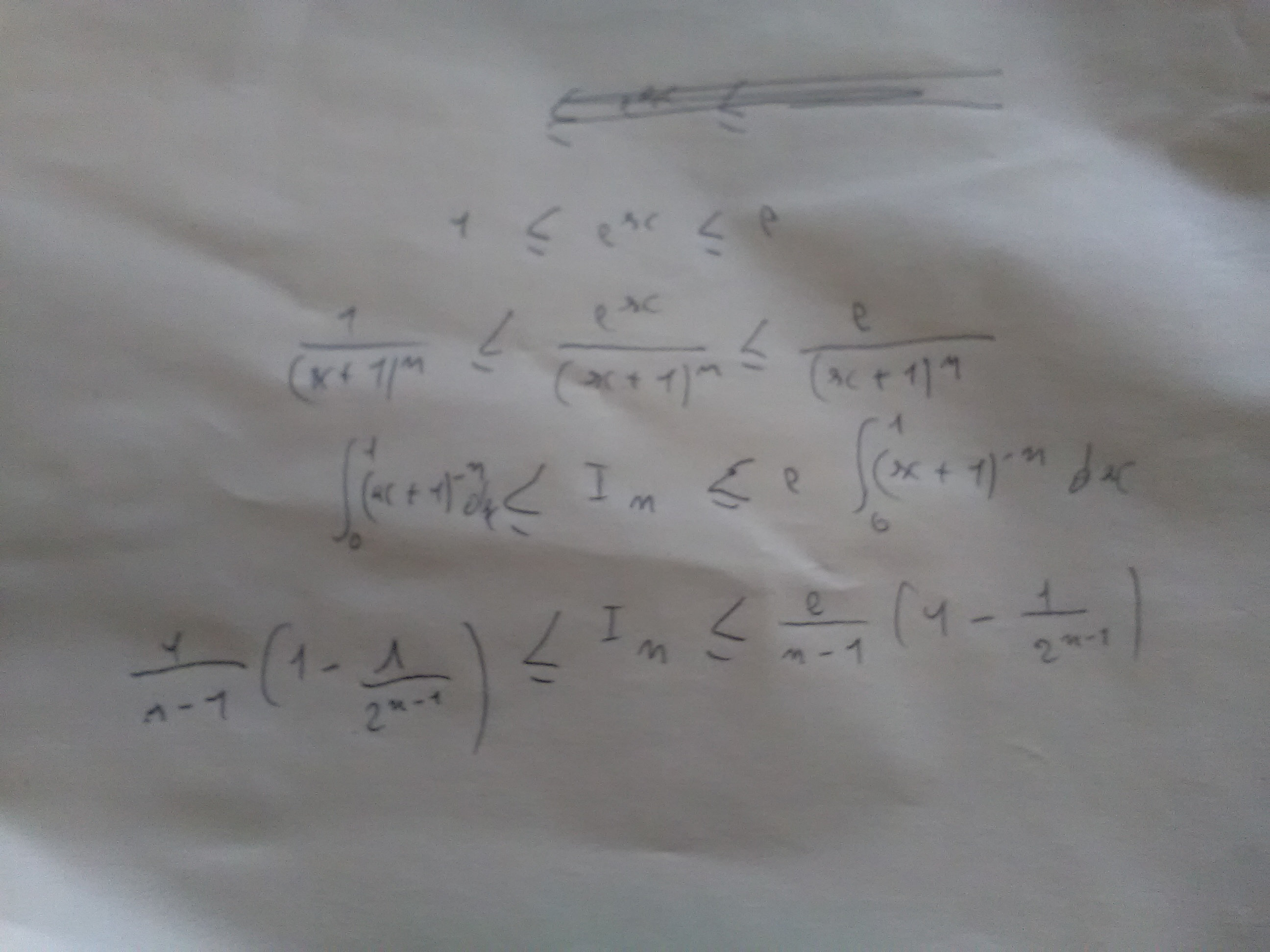
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités