Démontrer qu'une suite est géométrique
34 messages
- Page 1 sur 2 - 1, 2
Démontrer qu'une suite est géométrique
bonsoir, j'ai un gros problème, je dois démontrer que la suite ) définie par
définie par 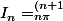\pi}e^{-t}sin t dt) est géométrique. J'ai essayé de calculer
est géométrique. J'ai essayé de calculer  pour pouvoir le retrouver quand je calculerai
pour pouvoir le retrouver quand je calculerai 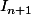 , mais avec le paramètre dans l'intégrale les calculs ne finnissent jamais a cause des dérivées de
, mais avec le paramètre dans l'intégrale les calculs ne finnissent jamais a cause des dérivées de 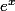 et les primitives de
et les primitives de 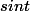 . J'ai essayé d'exprimer
. J'ai essayé d'exprimer 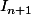 en fonction de
en fonction de  mais là aussi je n'ai rien obtenu de très convaincant, j'ai donc essayé avec la relation de Chasles mais ça ne m'avance pas non plus. Enfin 4e proposition, j'ai dit que
mais là aussi je n'ai rien obtenu de très convaincant, j'ai donc essayé avec la relation de Chasles mais ça ne m'avance pas non plus. Enfin 4e proposition, j'ai dit que ) est géométrique ssi il existe un réel q tel que
est géométrique ssi il existe un réel q tel que 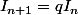 et je trouve
et je trouve -I_n}{I_n}) avec A(t) une intégrale différente de
avec A(t) une intégrale différente de  et
et 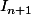 . Je m'en remets donc à vous pour m'aider à trouver une meilleure piste :doh:
. Je m'en remets donc à vous pour m'aider à trouver une meilleure piste :doh:
34 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
