Congruences
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 26 Mar 2014, 13:18
par upium666 » 26 Mar 2014, 13:18
Bonjour à tous et à toutes !
Résoudre dans
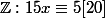
Je sais le faire quand c'est des petits modulos, à l'aide d'un tableau de restes, mais quand ça devient trop grand comme ici 20, je ne sais pas comment faire :/
Merci de m'aider
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 26 Mar 2014, 13:47
par Nightmare » 26 Mar 2014, 13:47
Bonjour,
tu peux t'en sortir en revenant à la définition des congruences :
15x = 5 mod 20 <=> 15x-5 = 0 mod 20 <=> 5(x-3)=0 mod 20 <=> 5(x-3) est nul ou est un multiple de 20.
5(x-3) nul fournit la solution x = 3
Pour 5(x-3) multiple de 20, on sait que 20 = 4*5 , donc pour que 5*(x-3) soit un multiple de 4*5, il faut et il suffit que (x-3) contienne un facteur 4, autrement dit que x-3 soit divisible par 4, donc que x = 3 mod 4
On vérifie dans le sens inverse que si x = 3 mod 4 alors 15x = 5 mod 20
C'est une méthode parmi d'autres, une autre consistant à essayer de faire comme dans R, essayer d'isoler x en multipliant 15x par des nombres qui permettent de se débarrasser de la multiplication par 15, autrement dit donner un sens à 1/15 (ce n'est pas possible ici, mais on peut donner un sens à 1/3 puis conclure presque immédiatement sachant que 15 = 3*5)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 146 invités