Equations avec congruences

par **Dinozzo13** » 20 Jan 2010, 15:55

Bonjour, en cours j'ai fait quelque équations avec des congruences mais je n'ai pas bien saisi leurs résolutions, ça me pose donc problème pour résoudre cette équation dans

:

.
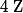
Voici par quoi j'ai commencé :

Cette équation admet des solutions si et seulement si le PGCD g,

, divise 0. Mais après, je vois pas comment faire :triste: .
Merci d'avance pour votre aide.

par **Skullkid** » 20 Jan 2010, 16:21

Bonjour,

Dinozzo13 a écrit:Cette équation admet des solutions si et seulement si le PGCD g, , divise 0.

Ta condition pour que ton équation ait des solutions dépend de la valeur de la variable, c'est un peu louche. De plus, tout nombre divise 0...

Sinon ça fait un bout de temps que j'ai pas résolu ce genre d'équation, mais c'est des équations du second degré qu'on résout dans ton cours ? Ton cours parle-t-il du théorème des restes chinois ?

par **Dinozzo13** » 20 Jan 2010, 16:23

Non, jamais entendu parler.
Mais oui, c'est le 2nd degré, le problème c'est que je n'ai fais que celles du 1er degrés.

par **Nightmare** » 20 Jan 2010, 16:24

Salut,

je comprends pas trop ta méthode mais voici quelque chose qui pourrait t'aider : 21 = 3*7

par **Dinozzo13** » 20 Jan 2010, 16:29

J'applique une méthode pour les équations du 1er degré, donc je fais avec ce que j'ai.

:ptdr: , j'y avais pensé mais je vois pas quoi en faire.

par **Skullkid** » 20 Jan 2010, 16:31

Dinozzo13 a écrit:Non, jamais entendu parler.
Mais oui, c'est le 2nd degré, le problème c'est que je n'ai fais que celles du 1er degrés.

Ah oui mais passer du premier au second degré c'est pas trivial, même dans

. Les méthodes de résolution ne se généralisent pas comme ça.

La seule méthode de résolution que je connaisse, et qui utilise d'ailleurs l'indication que t'a donnée Nightmare, passe par le théorème que je t'ai cité.

par **Nightmare** » 20 Jan 2010, 16:32

Si 21|3x²+4x, 3|3x²+4x et 7|3x²+4x

Continu.

par **Dinozzo13** » 20 Jan 2010, 16:35

Ah, il faut pas résoudre un système composé de ces deux équations ?
P.S.:
- le "|" veut dire est divise, non ?
- Que veut dire trivial :doh: ?

par **Skullkid** » 20 Jan 2010, 16:37

Trivial signifie évident, qui va de soi. Et | veut bien dire "divise" ^^

par **Dinozzo13** » 20 Jan 2010, 16:41

3|3x²+4x donc 3|x ou 3|3x+4
et
7|3x²+4x donc 7|x ou 7|3x+4
ok ?

par **Nightmare** » 20 Jan 2010, 16:43

Oui, par quel théorème?

par **Dinozzo13** » 20 Jan 2010, 16:46

Un théorème de divisibilité dans Z

par **benekire2** » 20 Jan 2010, 16:47

je n'ai jamais résolu d'équations du second degré avec congruence, mais je dirais qu'il faille tirer des conséquences directe de 3|x et 7|x et pareil pour les autres

par **Dinozzo13** » 20 Jan 2010, 16:51

Salut !
Je dirai que x est un multiple de 3 et de 7 donc de 21, ou que x est divisible par 3 et 7.

par **Skullkid** » 20 Jan 2010, 16:53

Grille pas d'étapes, pour l'instant t'en es à (7|x ou 7|3x+4) et (3|x ou 3|3x+4), donc t'es ramené à du premier degré.

par **benekire2** » 20 Jan 2010, 16:56

skull kid a raison :happy2: résous d'abord toutes ces équations puis tu tire des conséquences.

par **Dinozzo13** » 20 Jan 2010, 16:56

7|x ou 7|3x+4 donc

ou

par **Nightmare** » 20 Jan 2010, 16:58

On peut se débrouiller en partant de 3x²+4x=0[7] pour arriver à x²-x=0[7] dont les solutions sont alors triviales. Je vous laisse faire la transformation.

par **Dinozzo13** » 20 Jan 2010, 17:01

donc x est un multiple de 7 ou

Cette équation admet des solutions ssi le pgcd

divise 4, ce qui est le cas.

par **benekire2** » 20 Jan 2010, 17:01

Dinozzo13 a écrit:7|x ou 7|3x+4 donc ou

on peut faire mieux pour la deuxième, et de tête ( donc a vérifier ...) s'apprecevoir qu'il n'y a pas de solutions entières pour la deuxième.

Equations avec congruences

Equations avec congruences

Qui est en ligne