Equations avec congruences

par **Skullkid** » 20 Jan 2010, 20:10

Maintenant t'as plus qu'à tout regrouper, et t'auras les solutions de l'équation de départ :p

NB : une équation polynomiale aux congruences a soit aucune solution, soit une infinité. A partir du moment où t'as une solution x, tous les x+kn sont aussi solution (si tu travailles modulo n).

par **Dinozzo13** » 20 Jan 2010, 20:17

Avec tout ce qu'on a fait je suis un peu perdu, je ne peux donc pas regrouper tout ça.

par **Skullkid** » 20 Jan 2010, 23:38

Skullkid a écrit:On reprend donc, on en était à (7|x ou 7|3x+4) et (3|x ou 3|3x+4). On veut écrire ces différentes conditions plus simplement. Pour 7|x et 3|x, y en a pas besoin.

On cherche donc à trouver une condition équivalente à (ou impliquée par, quitte à vérifier après) 7|3x+4. Ça revient à résoudre 3x+4 = 0 [7], ce que tu sais faire si tu as eu un cours sur les équations du premier degré en congruences.

De même, résoudre 3|3x+4, ce qui n'est pas bien compliqué (pas besoin d'appliquer une méthode de résolution systématique).

Et depuis on a dit que 3|3x+4 n'a aucune solution, et que 7|3x+4 est équivalent à x = 1 [7] (quoique je suis pas sûr qu'on l'ait correctement justifié : la raison c'est que 7|3x+4 7|3x-3 7|3(x-1) 7|x-1 par Gauss).

par **Dinozzo13** » 21 Jan 2010, 06:28

Donc je reprends :

, c'est toujours vrai quelque soit

,

par **Ben314** » 21 Jan 2010, 08:36

Il me semble qu'il y a une erreur au début, on a :

Et la première équation n'a pas de solutions.

De plus, à la fin, tu doit donner le résultat sous la forme d'une unique congruence et pas sous la forme de multiples conditions.

par **benekire2** » 21 Jan 2010, 09:00

Il faut que tu reprenne de là ou on s'est arrêté et tu traite cas par cas, et tu devrais arriver a trouver ces solutions.

par **benekire2** » 21 Jan 2010, 09:05

donc( 3|x ou 3|3x+4 ) et ( 7|x ou 7|3x+4)
après réductions : 3|x et ( x=0[7] ou x=1[7] )
On a soit x=0[21] ou ( x=0[3] et x=1[7])
te reste plus qu'a étudier le deuxième cas. Par récurrence on doit y parvenir facilement.

par **Dinozzo13** » 21 Jan 2010, 11:35

En fait je viens de me rendre compte que je ne maitrisais peut-être pas assez la résolution d'équations du 1er degré avec congruence.
Le problème, c'est que je n'était pas là quand on a commencé les équations avec congruences donc si vous pouviez me dire de manière générale comment résoudre les équations de la forme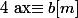

ce serait super sympa, parce que je ne comprends pas mon cours. Et donc de ce fait j'arriverai peut-être à faire cet exo.

par **Doraki** » 21 Jan 2010, 13:08

Tu peux toujours essayer à la main chaque valeur possible pour x modulo m.

Soit g le pgcd de a et de m.
Si ax = b mod m, alors ax+km = b pour un certain k donc g divise b.

Si g divise b alors on peut tout diviser par b et on est ramené à résoudre (a/g)x = (b/g) mod (m/g).
Si g ne divise pas b il n'y a pas de solution.

Donc on se ramène à étudier une équation ax = b mod m, où pgcd(a,m) = 1.
D'après bézout, il existe u et v tels que au+mv = 1, c'est à dire qu'on connaît un u tel que a*u = 1 modulo m.
En multipliant l'équation par ce u, on a que ax = b mod m implique x = b*u mod m. (et réciproquement en multipliant par a)

par **Ben314** » 21 Jan 2010, 13:19

Dans un cadre trés général, l'équation ax=b a pour unique solution x=b.a^{-1} lorsque
a est inversible , c'est à dire lorsqu'il existe un élément a' tel que a.a'=1.
Dans R ou C ou Q, tout les éléments non nuls sont inversible donc il n'y as pas de problème.
Par contre, pour les congruences, c'est un peu plus compliqué :
7 est inversible modulo 10 car 7x3=21=1 modulo 10 : l'inverse de 7 est 3
4 n'est pas inversible modulo 10 : 4*? ne peut être égal à 10k+1 (problème de parité) donc une équation 4x=? n'a pas forcément une unique solution modulo 10.
En fait un nombre a est inversible modulo n lorsqu'il existe a' et k tels que aa'=1+nk, c'est à dire aa'-kn=1 et c'est là que l'on voit (théorème de Bézout) que a est inversible modulo n si et seulement si n et a sont premier entre eux.
Par exemple, modulo 10, les inversibles sont 1 (d'inverse 1), 3 (d'inverse 7), 7 (d'inverse 3) et 9 (d'inverse 9) les nombres 0,2,5,6,8 ne sont pas inversibles.
Il est trés astucieux d'essayer de ne travailler qu'avec des congruences modulo un nombre premier p, car dans ce cas, tout les entiers de 1 à p-1 sont premier avec p donc inversible. On se retrouve alors avec la même chose que dans R ou C ou Q : tout nombre non nul est inversible.
Par exemple, modulo 7, seul 0 (modulo 7) n'est pas inversible. L'inverse de 1 est 1, celui de 2 et 4, celui de 3 est 5, celui de 4 est 2, celui de 5 est 3, celui de 6 est 6.

Par exemple, dans ton exo, tu doit résoudre 3x+4=0 modulo 7. Tu peut écrire :
3x+4=0 3x=-4 5.3x=5.-4 (on multiplie par l'inverse de 3 modulo 7 : c'est 5)
15x=-20 x=1 (car, modulo 7, on a 15=1 et -20=1)

par **Dinozzo13** » 21 Jan 2010, 14:45

Parce que moi, mon cours me dit qu'une équations de la forme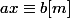

a une solution ssi le pgcd g de a et m divise b. Si a et m sont premiers entre eux alors l'équation a toujours une solution. Si

est une solution de cette équation alors toute autre solution s'écrit alors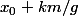

avec k entier relatif, donc je sais pas si ça suffit à résoudre ce genre d'équations.

par **Skullkid** » 21 Jan 2010, 15:03

Doraki a tout expliqué dans son post.

par **Dinozzo13** » 21 Jan 2010, 15:53

Je propose donc de faire quelque résolution d'équation de la forme

. Je te laisse en choisir 5 pour m'entrainer. Si tout va bien on essaiera plus dur et ensuite on reviendra à cet exo, est-tu d'accord ?
P.S. : J'ai que ça à faire cet aprem' :ptdr:

par **Doraki** » 21 Jan 2010, 15:58

ok lol
Donc résoud :

10x = 6 mod 1
10x = 6 mod 15
10x = 6 mod 16
10x = 6 mod 17
10x = 6 mod 23456789

par **Skullkid** » 21 Jan 2010, 15:58

Bah, tu peux prendre des valeurs de a, b et m au hasard, en essayant de varier un peu, genre qu'ils soient pas toujours premiers entre eux...

En jetant un dé :

3x = 2 (4)
5x = 1 (3)
2x = 5 (6)

par **Skullkid** » 21 Jan 2010, 16:02

Doraki a écrit:10x = 6 mod 23456789

P'tit joueur, on voit tout de suite que 2345679 est l'inverse de 10 modulo 23456789 :p

par **Dinozzo13** » 21 Jan 2010, 16:05

Bon, donc je résous, les équations suivantes :
3x = 2 (4)
5x = 1 (3)
2x = 5 (6)
10x = 6 mod 1
10x = 6 mod 15
10x = 6 mod 16
10x = 6 mod 17
10x = 6 mod 23456789
Je les fais et je vous tiens au courant, :++:

par **Dinozzo13** » 21 Jan 2010, 16:24

.

, pas de solutions.

.

, pas de solutions.

.

, pas de solutions.

, pas d'idée.

par **Skullkid** » 21 Jan 2010, 17:03

C'est juste (sauf erreur de ma part), sauf pour 10x = 6 (17) qui a bien des solutions (4 en est une).

Pour 10x = 6 (23456789) c'était une blague de Doraki, le modulo est trop grand pour qu'on puisse procéder de manière systématique à la main. Mais comme p = 23456789 est un nombre premier qui se termine par 9, l'inverse de 10 modulo p est facile à deviner : 10*2345679 = 1 (p). Donc les solutions c'est 2345679 + kp. Sans cette astuce tu es obligé de trouver l'inverse de 10 à la main...

Ça permet de voir que même les équations du premier degré peuvent être laborieuses à résoudre à la main, pour peu que le m soit grand et peu factorisable.

par **Doraki** » 21 Jan 2010, 17:14

En effet, 23456789 est premier, mais ça n'a pas d'importance. C'est juste qu'il se termine par 9, rendant l'inverse de 10 facile à vérifier.

Je voulais surtout voir s'il savait utiliser l'algorithme d'euclide, déjà pour trouver le pgcd, et après pour calculer les u et v dans l'égalité de Bézout.

Equations avec congruences

Qui est en ligne