Concours général 2014
17 messages
- Page 1 sur 1
concours général 2014
Bonsoir,
J'ai commencé le premier problème du cg 2014 mais je bloque sur la question 3-b.
Je pensais à une récurrence mais l'initialisation n'est pas évidente... et je vois pas comment faire autrement.
http://www.animath.fr/IMG/pdf/cgmaths2014.pdf
J'ai commencé le premier problème du cg 2014 mais je bloque sur la question 3-b.
Je pensais à une récurrence mais l'initialisation n'est pas évidente... et je vois pas comment faire autrement.
http://www.animath.fr/IMG/pdf/cgmaths2014.pdf
Ben314 a écrit:Salut,
Niveau term. (danc sans la notion de séries), je pense que le plus simple c'est d'encadrer Um-Un (pour m>n) puis de faire tendre m vers l'infini.
Merci !
Et j'ai un doute sur ma réponse à la question 2:
On peut supposer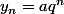 avec a un réel quelconque:
avec a un réel quelconque:
On alors alors-\bigsum_{k=0}^{n-1} q^{n-k-1}b_{k}\ge q^n(a-x_{0})-\frac{\epsilon}{1-q}) (j'ai pas mis les détails)
(j'ai pas mis les détails)
En prenant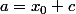 avec
avec 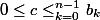 (sous réserve que les bk ne soient pas nuls et c'est ça qui me gêne) il existe alors une infinité de suite géometrique satisfaisant l'inégalité
(sous réserve que les bk ne soient pas nuls et c'est ça qui me gêne) il existe alors une infinité de suite géometrique satisfaisant l'inégalité
(car on a d'une part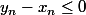 et de l'autre
et de l'autre \ge 0) et la décroissance de la fonction valeur absolue sur R- permet de conclure)
et la décroissance de la fonction valeur absolue sur R- permet de conclure)
On peut supposer
On alors alors
En prenant
(car on a d'une part
Et j'ai un doute sur ma réponse à la question 2:
On peut supposer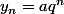 avec a un réel quelconque:
avec a un réel quelconque:
On alors alors-\bigsum_{k=0}^{n-1} q^{n-k-1}b_{k}\ge q^n(a-x_{0})-\frac{\epsilon}{1-q}) (j'ai pas mis les détails)
(j'ai pas mis les détails)
En prenant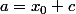 avec
avec 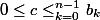 (sous réserve que les bk ne soient pas nuls et c'est ça qui me gêne) il existe alors une infinité de suite géometrique satisfaisant l'inégalité
(sous réserve que les bk ne soient pas nuls et c'est ça qui me gêne) il existe alors une infinité de suite géometrique satisfaisant l'inégalité
(car on a d'une part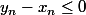 et de l'autre
et de l'autre \ge 0) et la décroissance de la fonction valeur absolue sur R- permet de conclure)
et la décroissance de la fonction valeur absolue sur R- permet de conclure)
On peut supposer
On alors alors
En prenant
(car on a d'une part
Déjà, sur la formulation, c'est pas terrible...
La question est "Montrer qu'il existe TRUC tel que"
A ce genre de question, on répond fréquemment : "Prenons (totalement par hasard... :zen:) TRUC =..."
Mais pas "On peut supposer que TRUC=..."
Ça :
Donc il faut se forcer à écrire "...avec c tel qu'il existe un entier n tel que..."
Sinon, sur le principe, ça va, mais effectivement ça ne te produit pas une infinité de solutions.
Perso :
a) J'aurais commencé par "Prenons comme suite géométrique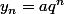 et regardons pour quelles valeurs de
et regardons pour quelles valeurs de  réel une telle suite convient"
réel une telle suite convient"
b) Le xn-yn, je l'aurais plutôt écrit dans l'autre sens (les majoration/minorations sur des négatifs... je me méfie...) :
+\bigsum_{k=0}^{n-1} b_k q^{n-1-k})
donc on a\leq u_n\leq q^n(x_{0}-a)+\frac{\varepsilon}{1-q}\) vu que
vu que 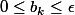
Donc, pour que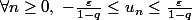 , il suffit que (et surtout pas "il faut que") :
, il suffit que (et surtout pas "il faut que") :
\) et
et +\frac{\varepsilon}{1-q}\leq \frac{\varepsilon}{1-q})
C'est à dire que}\) et que
et que 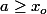 .
.
Or, comme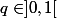 , la suite
, la suite _{n\geq 0}) est croissante donc pour que la première condition soit vérifiée, il suffit (là, on peut mettre "il faut et il suffit" si on veut, mais surtout pas seulement "il faut") que
est croissante donc pour que la première condition soit vérifiée, il suffit (là, on peut mettre "il faut et il suffit" si on veut, mais surtout pas seulement "il faut") que 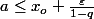
Il y a donc une infinité de qui conviennent.
qui conviennent.
La question est "Montrer qu'il existe TRUC tel que"
A ce genre de question, on répond fréquemment : "Prenons (totalement par hasard... :zen:) TRUC =..."
Mais pas "On peut supposer que TRUC=..."
Ça :
,bien qu'on comprenne le sens ,ça va pas non plus au niveau rédaction : tu fait comme si le c avait le droit de dépendre de n alors qu'il ne le doit pas (sinon a dépendrait de n et a.q^n ça serait plus une suite géométrique)t.itou29 a écrit:...avec...
Donc il faut se forcer à écrire "...avec c tel qu'il existe un entier n tel que..."
Sinon, sur le principe, ça va, mais effectivement ça ne te produit pas une infinité de solutions.
Perso :
a) J'aurais commencé par "Prenons comme suite géométrique
b) Le xn-yn, je l'aurais plutôt écrit dans l'autre sens (les majoration/minorations sur des négatifs... je me méfie...) :
donc on a
Donc, pour que
C'est à dire que
Or, comme
Il y a donc une infinité de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Déjà, sur la formulation, c'est pas terrible...
La question est "Montrer qu'il existe TRUC tel que"
A ce genre de question, on répond fréquemment : "Prenons (totalement par hasard... :zen:) TRUC =..."
Mais pas "On peut supposer que TRUC=..."
Ça :,bien qu'on comprenne le sens ,ça va pas non plus au niveau rédaction : tu fait comme si le c avait le droit de dépendre de n alors qu'il ne le doit pas (sinon a dépendrait de n et a.q^n ça serait plus une suite géométrique)
Donc il faut se forcer à écrire "...avec c tel qu'il existe un entier n tel que..."
Sinon, sur le principe, ça va, mais effectivement ça ne te produit pas une infinité de solutions.
Perso :
a) J'aurais commencé par "Prenons comme suite géométriqueet regardons pour quelles valeurs de
réel une telle suite convient"
b) Le xn-yn, je l'aurais plutôt écrit dans l'autre sens (les majoration/minorations sur des négatifs... je me méfie...) :
donc on avu que
Donc, pour que, il suffit que (et surtout pas "il faut que") :
et
C'est à dire queet que
.
Or, comme, la suite
est croissante donc pour que la première condition soit vérifiée, il suffit (là, on peut mettre "il faut et il suffit" si on veut, mais surtout pas seulement "il faut") que
Il y a donc une infinité dequi conviennent.
C'est vrai que c'est plus pratique de l'écrire dans ce sens...
J'ai minorée d'un côté mais j'ai pas du tout pensé à majorer de l'autre (à part avec 0 mais c'est pas efficace du tout), j'aurais du m'en douter avec la valeur absolue :mur:
Le truc (peut-être..) à voir, c'est qu'on arrive souvent à montrer ce type d'inégalité avec des valeur absolues en gardant tout le long les valeurs absolues, mais qu'il faut que les hypothèses soient elles aussi "en valeur absolues".
Alors que là, LA hypothèse, c'est que les beta_i sont entre 0 et epsilon et que si tu dit qu'il sont plus petit que epsilon en valeur absolue, tu perd trop d'information pour conclure (en fait, tu trouve que la suite yn=xo.q^n marche, mais c'est pas clair qu'il y en ait d'autres...)
Donc il faut "casser" la valeur absolue pour pouvoir utiliser "à fond" l'hypothèse.
Alors que là, LA hypothèse, c'est que les beta_i sont entre 0 et epsilon et que si tu dit qu'il sont plus petit que epsilon en valeur absolue, tu perd trop d'information pour conclure (en fait, tu trouve que la suite yn=xo.q^n marche, mais c'est pas clair qu'il y en ait d'autres...)
Donc il faut "casser" la valeur absolue pour pouvoir utiliser "à fond" l'hypothèse.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Je crois avoir trouvé la réponse au c :
On écrit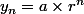 (avec a non nul)
(avec a non nul)
On a alors :
^n)|)
Pour que la suite convienne il faut donc que:
^n|\le\frac{\epsilon}{q^n(q-1)})
Si on fait tendre n vers l'infini, le membre droit tend vers 0 et 3 cas se présentent pour le membre gauche:
-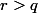 : il tend vers plus l'infini, impossible.
: il tend vers plus l'infini, impossible.
-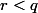 : il tend vers
: il tend vers 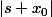 ce qui implique
ce qui implique 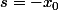 or
or  est strictement positif et s est positif, impossible.
est strictement positif et s est positif, impossible.
-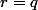 : il tend vers
: il tend vers 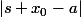 ce qui implique
ce qui implique 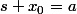
Dans ce cas on a bien d'après la question 3b):
})
Il me reste à montrer que a doit être non nul mais je pense que c'est facile, est-ce correct ?
On écrit
On a alors :
Pour que la suite convienne il faut donc que:
Si on fait tendre n vers l'infini, le membre droit tend vers 0 et 3 cas se présentent pour le membre gauche:
-
-
-
Dans ce cas on a bien d'après la question 3b):
Il me reste à montrer que a doit être non nul mais je pense que c'est facile, est-ce correct ?
Ben314 a écrit:C'est bon.
De plus, a est forcément non nul, sinon le membre de gauche de ton inégalité vaudrai à Un+Xo et ne tendrait pas vers 0 (cas identique à celui où r<q et tout aussi contradictoire)
D'accord, merci ! Et au fait à quoi réfère le titre "stabilité géométrique" ? J'arrive pas trop à "visualiser" le problème, à voir la suite en question.
Je pense que ça signifie qu'on étudie une suite "presque" géométrique dans le sens que x_{n+1} est "presque" égal à q.xn puis on regarde si ça implique qu'on puisse l'approximer par une vrai suite géométrique.
C'est en ce sens qu'on regarde la "stabilité" de la relation x_{n+1}=q.x_n
C'est en ce sens qu'on regarde la "stabilité" de la relation x_{n+1}=q.x_n
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Je pense que ça signifie qu'on étudie une suite "presque" géométrique dans le sens que x_{n+1} est "presque" égal à q.xn puis on regarde si ça implique qu'on puisse l'approximer par une vrai suite géométrique.
C'est en ce sens qu'on regarde la "stabilité" de la relation x_{n+1}=q.x_n
Ah ok, je vois. C'est pas mal comme problème, je préfère ça aux problèmes d'olympiades académiques avec leurs ruches d'abeilles et leurs routes à construire... (oui, j'ai détesté le sujet de cette année !)
Darkwolftech a écrit:Aha c'était quand même rigolo non ? :ptdr:
Rigolo c'est sur mais intéressant pas trop... mais je dois avouer que je ne suis pas très objectif: je voulais tout sauf de la géométrie et comme par hasard trois exos de géométrie ! :ptdr: Je dois quand même admettre que le tout premier problème avec la numérotation magique était plutôt pas mal.
t.itou29 a écrit:Rigolo c'est sur mais intéressant pas trop... mais je dois avouer que je ne suis pas très objectif: je voulais tout sauf de la géométrie et comme par hasard trois exos de géométrie ! :ptdr: Je dois quand même admettre que le tout premier problème avec la numérotation magique était plutôt pas mal.
Oui c'est vrai que niveau géometrie ... on a été servis ! :ptdr:
Tu es dans quelle académie ?
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
