N complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Sep 2006, 10:30
par Flodelarab » 01 Sep 2006, 10:30
une remarque que tu n'as pas faite (pardon si ça te paraissait évident):
2 est réel positif.
donc arg(2)=0
donc Arg(z-1/2) = 2Arg(z)
Maintenant je sais pas si ça t'aide
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 01 Sep 2006, 10:56
par nada-top » 01 Sep 2006, 10:56
alors là vraiment je sais pas ce qui me prend ce matin :mur:

A(1/2) alors
 \equiv (\vec{e_1} , \vec{OM}))
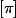
peut on en déduire qq chose enfin

-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Sep 2006, 11:15
par Flodelarab » 01 Sep 2006, 11:15
C pas etonnant de pleurer quand on se tape la tete contre un mur .... :wrong:
et il est passé ou le 2 ?
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 01 Sep 2006, 11:25
par nada-top » 01 Sep 2006, 11:25
 \equiv - 2 (\vec{OM} , \vec{e_1}) [\pi] \Leftrightarrow\;(\vec{OM} , \vec{e_1}) +(\vec{e_1} , \vec{AM}) \equiv -(\vec{OM} , \vec{e_1}) [\pi]\;\Leftrightarrow\; (\vec{OM}, \vec{AM}) \equiv (\vec{e_1} , \vec{OM}) [\pi])
non??
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Sep 2006, 11:36
par Flodelarab » 01 Sep 2006, 11:36
OK
On trouve donc R* ...
c ce que j'avais trouvé mais ça me parait bizarre
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 01 Sep 2006, 11:41
par nada-top » 01 Sep 2006, 11:41
tu veux dire l'axe des réels privé de o(0,0) , ça me oarit logique mais c'est pas tout car j'ai trouvé par l'autre méthode que l'ensempble de point est l'union de l'axe des réels privé de o(0,0) et
C(c'(1/2,0) , 1/2) .
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 01 Sep 2006, 11:51
par nada-top » 01 Sep 2006, 11:51
je trouve que l'ensemble de points est l'union de l'axe des réel privé de o(0,0) et C(c'(1/2,0) , 1/2) par l'autre méthode , mais je vois toujours pas ça avec cette dernière équivalence .
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 01 Sep 2006, 12:10
par fonfon » 01 Sep 2006, 12:10
Re, peut-être que pour ton exemple en posant z=x+iy c'est la methode la plus rapide pour l'ensemble des points je crois que c'est ça.
Pour l'autre methode j'y regarderai plus tard je dois partir
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Sep 2006, 12:12
par Flodelarab » 01 Sep 2006, 12:12
Ca me laisse perplexe.
Je trouve la réunion de R* et de Tous les points d'affixe: z=

ou z=

quand

Ce qui revient au meme
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 01 Sep 2006, 12:30
par nada-top » 01 Sep 2006, 12:30
je viens de vérifier pour la 2ème fois et je trouve encor que
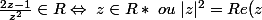)
en dévellopant

-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Sep 2006, 12:39
par Flodelarab » 01 Sep 2006, 12:39
On pourrait résumer par :
L'angle au centre est 2 fois l'angle inscrit, donc on décrit un cercle de centre A et de rayon 1/2 (pour passer par O) mais si l'arc intercepté est nul[

] alors tous les nombres conviennent (a part 0 évidemment)
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 01 Sep 2006, 12:52
par nada-top » 01 Sep 2006, 12:52
L'angle au centre est 2 fois l'angle inscrit, donc on décrit un cercle de centre A et de rayon 1/2 (pour passer par O)
on peut pas passer par O (
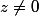
)
qu'est-ce que tu pense de :
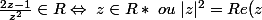)
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Sep 2006, 13:06
par Flodelarab » 01 Sep 2006, 13:06
hihihi
Tu fais la meme erreur (en exprimant la solution) que moi:
Je veux que le cercle passe par O mais j'exclus 0.
Tu réinclus 0 dans ta deuxième partie de solution
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 01 Sep 2006, 13:13
par nada-top » 01 Sep 2006, 13:13
Tu réinclus 0 dans ta deuxième partie de solution
moi j'ai

je crois que c suffisant pour dire que o est exclu :doh: je vois vraiment de quoi tu parle
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Sep 2006, 13:14
par Flodelarab » 01 Sep 2006, 13:14
c très logique ta conclusion car le cercle unité a pour propriété:
|z|²=1 <=> |z|=1 <=> cos²(t) + sin²(t) = 1 car z=cos(t) + i sin(t)
maintenant si je faire retrecir ce cercle de moitié:
z=cos(t)/2 + i sin(t)/2
et je le décale de 1/2:
z=cos(t)/2 + 1/2 + i sin(t)/2
alors |z|²= 1/2 |cos(t)+1 +i sin(t)| = 1/2 (cos²(t)+2cos(t)+1 + sin²(t))= cos(t)+1/2
... logique
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Sep 2006, 13:15
par Flodelarab » 01 Sep 2006, 13:15
nada-top a écrit:moi j'ai

je crois que c suffisant pour dire que o est exclu :doh: je vois vraiment de quoi tu parle
Oui mais tu dis:
OU |z|²=Re(z)
0 marche dans ce cas la
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 01 Sep 2006, 13:26
par nada-top » 01 Sep 2006, 13:26
Oui mais tu dis:
OU |z|²=Re(z)
0 marche dans ce cas la
je crois savoir que c'est un ou inclusif ... mais bon c'est une autre histoire :ptdr:
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Sep 2006, 13:31
par Flodelarab » 01 Sep 2006, 13:31
nada-top a écrit:je crois savoir que c'est un ou inclusif ... mais bon c'est une autre histoire :ptdr:
aïe!
Quel que soit la nature du "ou", ça permet pas a la moitié d'un membre de baver sur l'autre membre.
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 01 Sep 2006, 13:51
par nox » 01 Sep 2006, 13:51
nan mais pourquoi ca parle de baver sur les membres ici :ptdr:
un peu de tenue!!
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 01 Sep 2006, 13:53
par nada-top » 01 Sep 2006, 13:53
déjà dés le début li faut exclure le point o pour que l'expression soit vérifiée : donc
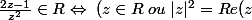 ) \;\mathcal{et}\; z\neq 0)
il y a un joli ''et'' là :lol2: donc il faut que les 2 propositions (entre le et) soient vraies .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
