Bonjour
Voilà mon exercice:
Soit G le centre de gravité du triangle ABC. Montrer que, pour tout point L du plan, (en vecteurs) MA+MB+MB=3MG
Merci!!
Complements sur le centre de gravité d'un triangle
4 messages
- Page 1 sur 1
Salut !
Par définition, est le centre de gravité du triangle
est le centre de gravité du triangle  signifie que
signifie que 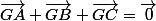 .
.
En introduisant le point dans les vecteurs
dans les vecteurs 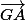 ,
, 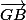 et
et 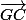 avec la relation de Chasles, tu auras
avec la relation de Chasles, tu auras  ,
,  et
et  et donc tu pourras aboutir au résultat voulu.
et donc tu pourras aboutir au résultat voulu.
:+++:
RMMS a écrit:Bonjour
Voilà mon exercice:
Soit G le centre de gravité du triangle ABC. Montrer que, pour tout point M du plan, (en vecteurs) MA+MB+MB=3MG
Merci!!
Par définition,
En introduisant le point
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
