On peut le faire "à la main" dans ce cas particulier là pour éventuellement mieux comprendre le truc :
Supposons que
=\infty)
.
On a donc
\!>\!A\big)\ \ (\star))
On se donne
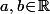
avec
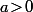
et on veut montrer que
=\infty)
, c'est à dire que
\!>\!B\big)\ (\star\star))
.
On commence évidement par se donner un
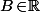
puis on cherche une condition suffisante (mais pas forcément nécessaire) de la forme
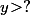
pour que
\!>\!B)
.
En comparant cette inégalité avec l'inégalité finale de
)
(qu'on sait être vraie), on voit que pour avoir un truc du même style, il faut "prendre"
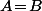
et
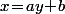
.
Le
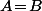
, y'a pas de soucis : la formule
)
commence par
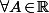
donc on peut parfaitement l'appliquer avec
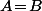
("le"

choisi au début du paragraphe) et on en déduit qu'il existe un
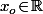
tel que, pour tout

dans

, on ait
\!>\!B\Big))
.
Maintenant, si

est un réel quelconque, alors il est bien clair que
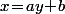
est lui même un réel et donc que
\!>\!B\Big))
.
Et il reste uniquement à voir que
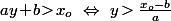
(car
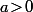
) pour réécrire la dernière implication sous la forme
\!>\!B\Big))
.
On vient donc de montrer que
\!>\!B\big))
ce qui prouve que la proposition
)
est vrai (il suffit de prendre
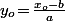
).
J'ai fait exprès d'absolument tout détailler "au cas où" : on peut évidement faire un raisonnement plus rapide, voire rédiger différemment pour obtenir (**) en partant de (*) plutôt que de "tourner autours du pot", sauf que quand on rédige de cette façon le
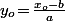
, on est obligé de "le sortir d'un chapeau" alors qu'avec cette rédaction bien plus longue, on comprend d'où il vient.
Sinon
LE truc à comprendre, c'est que lorsque tu traduit tes deux définitions de limites, il faut
absolument utiliser des lettres différentes, sinon tu ne comprend rien (ici, on a de la chance, le A et le B des deux définitions sont en fait "les mêmes", mais ils pourraient tout à fait être différents)
