Ah! JE suis content de lire que finalement tu comprends. C'est mieux que de seulement commencer.
Oui, je ne vois pas d'autre simplification (sauf erreur de ma part - ben oui hein désolé).
Etudier si une suite est monotone, cela revient à étudier ses varaitions. Pour voir dans quel sens une suite varie, le mieux est de calculer la diffèrence entre deux termes consécutifs et d'en étudier le signe.
A ton avis pourquoi depuis le début nous essayons de donner une expression générale pour

?
Et nous avons montré que l'expression générale de cette diffèrence est
^2} \left( n^2-2.n-1\right))
?
Comme je n'ai pas oublié de mettre n au carré, on se rend compte
que
^2})
est strictement positif pour tout
n de
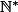
Donc le signe de la diffèrence entre deux termes consécutifs de la suite dépend de ...
