Calcul de la tangente commune a 2 cercles
22 messages
- Page 1 sur 2 - 1, 2
Calcul de la tangente commune a 2 cercles
Bonjour à tous,
Je suis plombier, je cherche à concevoir un outil pour m'aider à façonner le cuivre. Comme le titre de mon post l'indique je cherche à calculer la tangente commune a deux cercles dont j'ai les coordonnés X;Y ainsi que le diamètre de chacun.
Je suis pas très bon en math, si une âme charitable passe par là pour m'aider ce serait très sympa.
Merci !
Je suis plombier, je cherche à concevoir un outil pour m'aider à façonner le cuivre. Comme le titre de mon post l'indique je cherche à calculer la tangente commune a deux cercles dont j'ai les coordonnés X;Y ainsi que le diamètre de chacun.
Je suis pas très bon en math, si une âme charitable passe par là pour m'aider ce serait très sympa.
Merci !
bulldog33 a écrit:Bonjour à tous,
Je suis plombier, je cherche à concevoir un outil pour m'aider à façonner le cuivre. Comme le titre de mon post l'indique je cherche à calculer la tangente commune a deux cercles dont j'ai les coordonnés X;Y ainsi que le diamètre de chacun.
Je suis pas très bon en math, si une âme charitable passe par là pour m'aider ce serait très sympa.
Merci !
Bonjour,
Ce sont les coordonnées des centres des 2 cercles que tu as ? Dans ce cas, ce problème n'a une solution que si la distance entre ces 2 points est égale à la somme des rayons (soit les demi-diamètres) des 2 cercles.
PSEUDA a écrit:Bonjour,
Ce sont les coordonnées des centres des 2 cercles que tu as ? Dans ce cas, ce problème n'a une solution que si la distance entre ces 2 points est égale à la somme des rayons (soit les demi-diamètres) des 2 cercles.
Bonjour !
Merci pour votre réponse les coordonnées sont bien celle des deux cercles. La distance entre les 2 cercles est égale a deux rayons + 0.5 sur X
mathelot a écrit:est ce que c'est:
(1) une droite tangente commune avec des points de tangence distincts
ou
(2) deux cercles tangents avec un unique point de tangence
Il s'agit du (1) une droite tangente commune un points de tangence sur chaque cercle
http://www.ilemaths.net/img/forum_img/0405/forum_405110_1.jpg
bulldog33 a écrit:Il s'agit du (1) une droite tangente commune un points de tangence sur chaque cercle
http://www.ilemaths.net/img/forum_img/0405/forum_405110_1.jpg
Ok, je n'avais pas compris. Dans ce cas, il faut appliquer le théorème de Thalès étant donné que (AM) est parallèle à (PB), toutes deux orthogonales à la tangente commune.
On a alors : OA / OB = OM / OP = AM / BP = 2/3.
Il faut donc prendre 2/5 sur (AB) en partant de A pour obtenir O, autrement dit diviser le segment [AB] en 5 et placer O à 2/5 de A : pour chaque coordonnée x et y : x0 = xa + 2/5 (xb-xa), idem pour y.
Puis pour obtenir M et P, il n'y a plus qu'à tracer les cercles de diamètres [OA] et [OB]. Ils coupent les 2 cercles en M et P (à noter qu'il y a 2 tangentes communes, la droite (AB) étant axe de symétrie de la figure).
Faut-il traduire ceci par des coordonnées ou par l'équation de la droite (MP) ?
PSEUDA a écrit:Ok, je n'avais pas compris. Dans ce cas, il faut appliquer le théorème de Thalès étant donné que (AM) est parallèle à (PB), toutes deux orthogonales à la tangente commune.
On a alors : OA / OB = OM / OP = AM / BP = 2/3.
Il faut donc prendre 2/5 sur (AB) en partant de A pour obtenir O, autrement dit diviser le segment [AB] en 5 et placer O à 2/5 de A : pour chaque coordonnée x et y : x0 = xa + 2/5 (xb-xa), idem pour y.
Puis pour obtenir M et P, il n'y a plus qu'à tracer les cercles de diamètres [OA] et [OB]. Ils coupent les 2 cercles en M et P (à noter qu'il y a 2 tangentes communes, la droite (AB) étant axe de symétrie de la figure).
Faut-il traduire ceci par des coordonnées ou par l'équation de la droite (MP) ?
Super !! Merci pour ton aide ce sont des coordonnes qu'il me faudrait. Le but étant de réaliser une application smartphone qui calcul l'épure d'un chapeau de gendarme en cuivre !
MABYA a écrit:les coordonnées de M et P ou l'équation d M ?
Où places tu tes axes de repère ?
il serait plus facile d'avoir AB comme abscisse avec A pour origine.
Bonsoir MABYA,
J'ai réalisé une petite image qui représente exactement mon cas de figure :
http://hpics.li/240f59e
Je dois trouver les coordonnées des points M et P.
Je précise que le rayon des cercles est connu et que A et B ont le même rayon.
bulldog33 a écrit:Bonsoir MABYA,
J'ai réalisé une petite image qui représente exactement mon cas de figure :
http://hpics.li/240f59e
Je dois trouver les coordonnées des points M et P.
Je précise que le rayon des cercles est connu et que A et B ont le même rayon.
Bonjour bulldog33,
La formule des coordonnées de M et P en fonction de celles de A et B et du rayon R est assez compliquée, je vais essayer de la transcrire ici en TEX.
Comme les rayons des cercles sont égaux, on a O au milieu de [AB] :
Tu en déduis
Voilà !
PSEUDA a écrit:Bonjour bulldog33,
La formule des coordonnées de M et P en fonction de celles de A et B et du rayon R est assez compliquée, je vais essayer de la transcrire ici en TEX.
Comme les rayons des cercles sont égaux, on a O au milieu de [AB] :et
. R est le rayon des cercles, OA = (demi-distance AB) =
Tu en déduiset
. Pour P, les formules sont les mêmes, sauf qu'il faut les multiplier par un "-".
Voilà !
PSEUDA je vous remercie infiniment, j'ai réussi grâce à votre aide et je tiens à vous remercier pour l'aide que vous m'avez apporté !!!!!
bulldog33 a écrit:PSEUDA je vous remercie infiniment, j'ai réussi grâce à votre aide et je tiens à vous remercier pour l'aide que vous m'avez apporté !!!!!
Je me permet de revenir vers vous car je rencontre un soucis.
Lorsque les deux cercles se trouvent sur le meme Y pas de soucis ça fonctionne, par contre si ils sont décalés là ça ne fonctionne plus : http://hpics.li/3fdf0e3
Les points n'appartiennent plus aux cercles.
Ci dessous l'interprétation des formules en javascript.
- Code: Tout sélectionner
var FCA = new Object();
FCA.x = 400;
FCA.y = 300;
var FCB = new Object();
FCB.x = 625;
FCB.y = 200;
var o = new Object();
o.x = (FCA.x + FCB.x) / 2;
o.y = (FCA.y + FCB.y) / 2;
o.a = Math.sqrt( ((FCA.x - FCB.x) * (FCA.x - FCB.x)) + ((FCA.y - FCB.y) * (FCA.y - FCB.y))) / 2;
var tangente = new Array();
var x, y;
x = ((FCA.x - FCB.x) / 2) * (1 - ((rc * rc) / (o.a * o.a))) + ((FCA.y - FCB.y) / 2) * (rc / o.a) * Math.sqrt( 1 - ((rc * rc) / (o.a * o.a)));
y = ((FCA.x - FCB.x) / 2) * (rc / o.a) * Math.sqrt((1 - ((rc * rc) / (o.a * o.a)))) + ((FCA.y - FCB.y) / 2) * (1 - ((rc * rc) / (o.a * o.a)));
x += o.x;
y += o.y;
tangente[0] = new Object({x : x, y: y});
x = -(((FCA.x - FCB.x) / 2) * (1 - ((rc * rc) / (o.a * o.a))) + ((FCA.y - FCB.y) / 2) * (rc / o.a) * Math.sqrt( 1 - ((rc * rc) / (o.a * o.a))));
y = -(((FCA.x - FCB.x) / 2) * (rc / o.a) * Math.sqrt((1 - ((rc * rc) / (o.a * o.a)))) + ((FCA.y - FCB.y) / 2) * (1 - ((rc * rc) / (o.a * o.a))));
x += o.x;
y += o.y;
tangente[1] = new Object({x : x, y: y});
bulldog33 a écrit:Je me permet de revenir vers vous car je rencontre un soucis.
Lorsque les deux cercles se trouvent sur le meme Y pas de soucis ça fonctionne, par contre si ils sont décalés là ça ne fonctionne plus : http://hpics.li/3fdf0e3
Les points n'appartiennent plus aux cercles.
Ci dessous l'interprétation des formules en javascript.
- Code: Tout sélectionner
var FCA = new Object();
FCA.x = 400;
FCA.y = 300;
var FCB = new Object();
FCB.x = 625;
FCB.y = 200;
var o = new Object();
o.x = (FCA.x + FCB.x) / 2;
o.y = (FCA.y + FCB.y) / 2;
o.a = Math.sqrt( ((FCA.x - FCB.x) * (FCA.x - FCB.x)) + ((FCA.y - FCB.y) * (FCA.y - FCB.y))) / 2;
var tangente = new Array();
var x, y;
x = ((FCA.x - FCB.x) / 2) * (1 - ((rc * rc) / (o.a * o.a))) + ((FCA.y - FCB.y) / 2) * (rc / o.a) * Math.sqrt( 1 - ((rc * rc) / (o.a * o.a)));
[B] y = ((FCA.x - FCB.x) / 2) * (rc / o.a) [/B]* Math.sqrt((1 - ((rc * rc) / (o.a * o.a)))) + ((FCA.y - FCB.y) / 2) * (1 - ((rc * rc) / (o.a * o.a)));
x += o.x;
y += o.y;
tangente[0] = new Object({x : x, y: y});
x = -(((FCA.x - FCB.x) / 2) * (1 - ((rc * rc) / (o.a * o.a))) + ((FCA.y - FCB.y) / 2) * (rc / o.a) * Math.sqrt( 1 - ((rc * rc) / (o.a * o.a))));
y = -(((FCA.x - FCB.x) / 2) * (rc / o.a) * Math.sqrt((1 - ((rc * rc) / (o.a * o.a)))) + ((FCA.y - FCB.y) / 2) * (1 - ((rc * rc) / (o.a * o.a))));
x += o.x;
y += o.y;
tangente[1] = new Object({x : x, y: y});
J'ai re-vérifié ma formule, elle me paraît correcte. Dans ta formule de y en Java, n'aurais-tu pas oublié le - qui suit le signe égal ?
Pour les points que tu indiques dans Java, j'obtiens :
Point M Point P
497,9157223 527,0842777
320,3103751 179,6896249
PSEUDA a écrit:J'ai re-vérifié ma formule, elle me paraît correcte. Dans ta formule de y en Java, n'aurais-tu pas oublié le - qui suit le signe égal ?
Pour les points que tu indiques dans Java, j'obtiens :
Point M Point P
497,9157223 527,0842777
320,3103751 179,6896249
Effectivement je suis désolé vous avez raison j'ai oublié le (-), tout fonctionne parfaitement à présent !
bulldog33 a écrit:Effectivement je suis désolé vous avez raison j'ai oublié le (-), tout fonctionne parfaitement à présent !
En réalité, il y a en général 4 tangentes communes à 2 cercles suffisamment éloignés, deux tangentes "intérieures" et deux "extérieures". Celle-là n'est que l'une des 2 intérieures, celle où l'angle formé par les demi-droites [OA) et [OM) a sa mesure principale négative, c'est-à-dire qu'on part de [OA) pour aller vers [OM) dans le sens des aiguilles d'une montre.
Tu peux avoir les coordonnées des points de contact de l'autre tangente intérieure en modifiant les signes dans les formules. Si tu en as besoin, je me ferais un plaisir de te répondre. :lol3:
bulldog33 a écrit:Bonjour à tous,
Je suis plombier, je cherche à concevoir un outil pour m'aider à façonner le cuivre. Comme le titre de mon post l'indique je cherche à calculer la tangente commune a deux cercles dont j'ai les coordonnés X;Y ainsi que le diamètre de chacun.
Je suis pas très bon en math, si une âme charitable passe par là pour m'aider ce serait très sympa.
Merci !
Bonjour tout le monde,
Bonjour bulldog33,
Je dois être en retard d'un monde..
Un plombier pas trop fort en math (dixit) qui fait une application en java pour smartphone..
Sincères félicitations.
PSEUDA a écrit:Bonjour bulldog33,
La formule des coordonnées de M et P en fonction de celles de A et B et du rayon R est assez compliquée, je vais essayer de la transcrire ici en TEX.
Comme les rayons des cercles sont égaux, on a O au milieu de [AB] :et
. R est le rayon des cercles, OA = (demi-distance AB) =
Tu en déduiset
. Pour P, les formules sont les mêmes, sauf qu'il faut les multiplier par un "-".
Voilà !
Salut,
Juste par curiosité comment as-tu trouvé la formule ? J'ai retrouvé quelque chose de semblable en passant par les rotations mais c'est ça fait pas mal de calculs, il y a-t-il plus simple ?
t.itou29 a écrit:Salut,
Juste par curiosité comment as-tu trouvé la formule ? J'ai retrouvé quelque chose de semblable en passant par les rotations mais c'est ça fait pas mal de calculs, il y a-t-il plus simple ?
C'est aussi par la rotation du vecteur OA d'angle (OA,OM) puis par l'homothétie de centre O et de rapport OM /OA. Cela fait pas mal de calculs en effet.
Je sais pas si ça fait vraiment moins de calculs, mais perso, j'aurais écrit qu'on cherche  et
et  tels que
tels que  ;
;  et
et  c'est à dire
c'est à dire 
C'est à dire en fait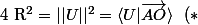)
Si) , qu'on pose
, qu'on pose ) et qu'on cherche
et qu'on cherche  sous la forme
sous la forme  alors la double équation (*) devient :
alors la double équation (*) devient :
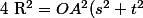=OA^2s\) qui donne immédiatement
qui donne immédiatement  et
et 
Bilan, si le point cherché est P alors
C'est à dire en fait
Si
Bilan, si le point cherché est P alors
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
