Tangente commune et exponentielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 08 Nov 2012, 23:17
par bentaarito » 08 Nov 2012, 23:17
si


comment traduire D1=D2 ?
-
Guiguidu60
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Nov 2012, 20:41
-
 par Guiguidu60 » 08 Nov 2012, 23:26
par Guiguidu60 » 08 Nov 2012, 23:26
bentaarito a écrit:si


comment traduire D1=D2 ?
Je vois pas comment ecrire ça avec les équations je sais qu'elles ont le meme coeff et au moins un point en commun mais je sais pas ou plus l'écrire avec les équations
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 08 Nov 2012, 23:31
par bentaarito » 08 Nov 2012, 23:31
il faut qu il ait mm coef dir -->a1=a2
et un point en commun --> b1=b2
-
Guiguidu60
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Nov 2012, 20:41
-
 par Guiguidu60 » 08 Nov 2012, 23:33
par Guiguidu60 » 08 Nov 2012, 23:33
bentaarito a écrit:il faut qu il ait mm coef dir -->a1=a2
et un point en commun --> b1=b2
OK merci ! Mais après avec ces deux égalité ont fais quoi ?
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 08 Nov 2012, 23:54
par bentaarito » 08 Nov 2012, 23:54
Guiguidu60 a écrit:OK merci ! Mais après avec ces deux égalité ont fais quoi ?
tu appliques ça pour tes tangentes
t es censé trouver le resultat donné par chan97
-
Guiguidu60
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Nov 2012, 20:41
-
 par Guiguidu60 » 09 Nov 2012, 00:28
par Guiguidu60 » 09 Nov 2012, 00:28
bentaarito a écrit:tu appliques ça pour tes tangentes
t es censé trouver le resultat donné par chan97
Donc on a
exp(a)=exp(-b-1)
exp(a)=-exp(-b-1)
exp(-b-1)=-exp(-b-1) ---> on trouve b
et après on se sert des équations du dessus
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 09 Nov 2012, 00:51
par bentaarito » 09 Nov 2012, 00:51
Guiguidu60 a écrit:Donc on a
exp(a)=exp(-b-1)
exp(a)=-exp(-b-1)
exp(-b-1)=-exp(-b-1) ---> on trouve b
et après on se sert des équations du dessus
Pourquoi exp(a)=-exp(-b-1) ?
c'est quoi l'ordonnée à l origine de
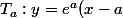+e^a)
-
Guiguidu60
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Nov 2012, 20:41
-
 par Guiguidu60 » 09 Nov 2012, 01:01
par Guiguidu60 » 09 Nov 2012, 01:01
[quote="bentaarito"]Pourquoi exp(a)=-exp(-b-1) ?
c'est quoi l'ordonnée à l origine de
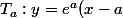+e^a)
[/
:mur: je me suis trompé j'ai pas les bonnes ordonnées à l'origine
Après corrections on a
exp(a)=exp(-b-1)
-exp(a)*a+exp(a)=-exp(-b-1)*b-exp(-b-1)
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 09 Nov 2012, 01:05
par bentaarito » 09 Nov 2012, 01:05
très bien
que donne exp(a)=exp(-b-1)?
-
Guiguidu60
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Nov 2012, 20:41
-
 par Guiguidu60 » 09 Nov 2012, 01:17
par Guiguidu60 » 09 Nov 2012, 01:17
bentaarito a écrit:très bien
que donne exp(a)=exp(-b-1)?
J'arrive pas à isoler dans la 2 eme égalité exp (a) pour pouvoir remplacer dans la première et ensuite avoir que b comme inconnu
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 09 Nov 2012, 01:32
par bentaarito » 09 Nov 2012, 01:32
Guiguidu60 a écrit:J'arrive pas à isoler dans la 2 eme égalité exp (a) pour pouvoir remplacer dans la première et ensuite avoir que b comme inconnu
par bijectivité de lexponentielle, exp(a)=exp(-b-1) a=-b-1
remplace dans (2) pour résoudre le système dans son intégralité
-
Guiguidu60
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Nov 2012, 20:41
-
 par Guiguidu60 » 09 Nov 2012, 01:58
par Guiguidu60 » 09 Nov 2012, 01:58
bentaarito a écrit:par bijectivité de lexponentielle, exp(a)=exp(-b-1) a=-b-1
remplace dans (2) pour résoudre le système dans son intégralité
je trouve
b=exp(-b-1)-1
a=-exp(-b-1)
est ce correcte
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 09 Nov 2012, 07:48
par bentaarito » 09 Nov 2012, 07:48
(1): exp(a)=exp(-b-1)<--> a=-b-1
on remplace exp(-b-1) par exp(a) dans :
(2): -exp(a)a+exp(a)=-exp(-b-1)b-exp(-b-1)
ça donne :
-exp(a)a+exp(a)=-exp(a)b-exp(a) <--> -a+1=-b-1
on remplace b par -a-1:
-a+1=-b-1<-->-a+1=a+1-1<-->a=1/2

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 09 Nov 2012, 09:47
par chan79 » 09 Nov 2012, 09:47
Guiguidu60 a écrit:je trouve
b=exp(-b-1)-1
a=-exp(-b-1)
est ce correcte
Bonjour
Je reprends
Supposons qu'une droite soit tangente à C au point A(a,b) et tangente à C' au point A'(a',b')
La pente de cette droite est d'une part f'(a) et d'autre part g'(a') .
f'(x)=

donc f'(a)=
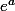
g'(x)=

donc g'(a')=

on a donc
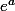
=

soit a=-a'-1
A(a,
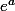
)
A'(a',-

)
A'(-a-1,-
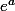
)
La droite (AA') passe par le milieu de [AA'] qui a comme abscisse (a-a-1)/2=-1/2 et comme ordonnée 0
L'équation de la tangente est y-
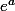
=
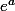
(x-a)
pour x=-1/2 on a y=0
-
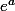
=
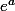
(-1/2-a)
-1=-1/2-a donc a=1/2
L'équation est y-
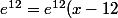)
y=
)
Coordonnées des points de contact
A(
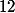
;

)
A'(

;

)
-
Guiguidu60
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Nov 2012, 20:41
-
 par Guiguidu60 » 09 Nov 2012, 10:58
par Guiguidu60 » 09 Nov 2012, 10:58
bentaarito a écrit:(1): exp(a)=exp(-b-1) a=-b-1
on remplace exp(-b-1) par exp(a) dans :
(2): -exp(a)a+exp(a)=-exp(-b-1)b-exp(-b-1)
ça donne :
-exp(a)a+exp(a)=-exp(a)b-exp(a) -a+1=-b-1
on remplace b par -a-1:
-a+1=-b-1-a+1=a+1-1a=1/2
Une fois que tu as a et b tu les remplace dans les équations de tangente ?
Et comment passes-tu de a=b-1 à -a+1=-b-1
-
Guiguidu60
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Nov 2012, 20:41
-
 par Guiguidu60 » 09 Nov 2012, 11:57
par Guiguidu60 » 09 Nov 2012, 11:57
Guiguidu60 a écrit:Une fois que tu as a et b tu les remplace dans les équations de tangente ?
Et comment passes-tu de a=b-1 à -a+1=-b-1
Pour finir l'exercice j'ai fait comme ceci :
On calcule l'image de points a et b
A(1/2;exp(1/2))
B(-3/2;-exp(1/2))
Les points A et B appratiennent à une même doite de coeff dir exp(1/2)
y=m x + p
-exp(1/2)= exp(1/2) * -3/2 + p
-1=-3/2+p
1/2=p
donc y = exp(1/2)*x+1/2
Donc le deux courbes admettent un tangente commune d'équation y = exp(1/2)*x+1/2
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 10 Nov 2012, 09:50
par bentaarito » 10 Nov 2012, 09:50
Guiguidu60 a écrit:Une fois que tu as a et b tu les remplace dans les équations de tangente ?
Et comment passes-tu de a=b-1 à -a+1=-b-1
tu simplifies par exp(a)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
