Calcul de primitive

[nico033]

Bonjour , j'ai un calcul de primitive que je narrive pas a faire pourriez vous maider sil vous plait

il faut que je trouve la primitive de :

A = (2x)/(x²-1)².

[fonfon]

salut tu ne trouves pas que c'est de la forme donc ...

[nico033]

je ne connais pas la primitive de u/u² pourriez vous me la donner sil vous plait

et il faut aussi que je trouve la primitive de

(1)/(1+exp(x))
pourriez vous maider sil vous plait

[nico033]

ah ca yest jai peut trouvé cela ne serrait pas:

F(x) = x²*((x²-1)^(-2+1))/(-2+1) + C
d'où F(x) = x² * ((x²-1)^-1)/(-1) + C
F(x) = x² * (-1)/(x²-1) + C
est cela?
par contre pour la primitive de (1)/(1+exp(x))
je ne vois pas

[fonfon]

ah ca yest jai peut trouvé cela ne serrait pas:

F(x) = x²*((x²-1)^(-2+1))/(-2+1) + C
d'où F(x) = x² * ((x²-1)^-1)/(-1) + C
F(x) = x² * (-1)/(x²-1) + C
est cela?

non, c'est pas ça

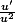
si f est de la forme alors

donc ici on pose u(x)=x²-1 donc u'(x)=2x
donc f(x)=u'(x)/u²(x) donc


je regarde l'autre

[fonfon]

il faut aussi que je trouve la primitive de

(1)/(1+exp(x))

c'est etonnant que l'on te donne ça sans questions préalables enfin il faut que tu transformes



ensuite dans on reconnait u'/u donc...

[nico033]

la primtive de u'/ est ln u
donc F(x) = ln(exp(x)+1). est ce ca?

[fonfon]

la primtive de u'/ est ln u
donc F(x) = ln(exp(x)+1). est ce ca?

presque c'est ln|u| car tout depend de u et de l'intervalle où tu travailles ici e^x+1>0 donc pas besoin des | |

tu as oublier un morceau c'est f(x)=1-e^x/(e^x+1)

F(x)=x-ln(e^x+1)+k