Calcul intégral - Primitive
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
JBrother
- Messages: 9
- Enregistré le: 28 Juil 2007, 08:35
-
 par JBrother » 11 Aoû 2007, 16:35
par JBrother » 11 Aoû 2007, 16:35
Bonjour, Quelqu'un serai assez aimbable pr me dire si mes calculs sont corrects?
Merci par avance

-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 11 Aoû 2007, 17:01
par anima » 11 Aoû 2007, 17:01
JBrother a écrit:Bonjour, Quelqu'un serai assez aimbable pr me dire si mes calculs sont corrects?
Merci par avance

dx)
correct
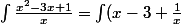dx = \frac{x^2}{2}-3x+ln|x|+k)
Preuve:
}{dx} = x-3+\frac{1}{x} = \frac{x^2}{x}-\frac{3x}{x}+\frac{1}{x} = \frac{x^2-3x+1}{x})
^4} = \int \frac{1}{2} \frac{2x}{(x^2+1)^4} \\<br />= \int \frac{1}{2} (x^2+1)^-4 (x^2+1)' \\<br />= -\frac{1}{6} (x^2+1)^-3 +k)
sauf erreur de ma part
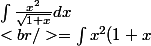^{-\frac{1}{2}}dx)
I.P.P:
u = x^2 -> u'=2x
v' = (1+x)^-0.5 -> v=2(1+x)^{0.5}

Seconde I.P.P:
u = x -> u' = 1
v' = (1+x)^0.5 -> v = 2/3(1+x)^1.5
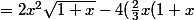^{\frac{3}{2}} - \int \frac{2(1+x)^{1.5}}{3}dx) \\<br />= 2x^2\sqrt{1+x}-4(\frac{2}{3}x(1+x)^{\frac{3}{2}} - \frac{2}{5}\frac{2(1+x)^{2.5}}{3}))
Sauf erreur de ma part pour la derniere.
-
maf
- Membre Rationnel
- Messages: 911
- Enregistré le: 08 Jan 2007, 17:57
-
 par maf » 11 Aoû 2007, 18:47
par maf » 11 Aoû 2007, 18:47
Bonjour,
JBrother, tu as fais une erreur à la 3ème : quand tu re-remplace a, tu mets x+2 au lieu de x^2+1
Anima, apparemment pour la dernière, il y a un carré sous la racine
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 11 Aoû 2007, 19:06
par anima » 11 Aoû 2007, 19:06
maf a écrit:Bonjour,
JBrother, tu as fais une erreur à la 3ème : quand tu re-remplace a, tu mets x+2 au lieu de x^2+1
Anima, apparemment pour la dernière, il y a un carré sous la racine
Et j'ai encore sauté un carré.
-
maf
- Membre Rationnel
- Messages: 911
- Enregistré le: 08 Jan 2007, 17:57
-
 par maf » 11 Aoû 2007, 19:08
par maf » 11 Aoû 2007, 19:08
Personnelement j'obtien pour réponse :

-
maf
- Membre Rationnel
- Messages: 911
- Enregistré le: 08 Jan 2007, 17:57
-
 par maf » 11 Aoû 2007, 19:29
par maf » 11 Aoû 2007, 19:29
je propose pour la dernière de poser x = shm donc puisque chm positif,

dx = chm dm
on obtient donc l'intégrale suivante :

posons maintenant 2m = n -> dm = dn/2
sachant que :
 = \frac {chx-1}{2})
On obtiens :

Puisque x = shm = sh(n/2) --> n = 2arshx
On a alors :
-2arshx}{4})
+ k
si je me trompe pas : 2arshx = arsh^2(x) d'où
On a alors :

+ k
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités

