Bijectivité argument de la diagonale Cantor

[jankyjack]

bonjour,

j'essaie de demontrer la bijectivité de la l'argument de la diagonale de cantor mais c'est un peu complexe puisqu'en fait je la considere comme une fonction ayant deux parametres et comment on fait pour demontrer qui a deux parametres est bijective.

la diagonale en question est dc(m, n)= =1/2(m + n)(m + n +1) + m.
je vous remercie déjà pour vos réponses

[Ben314]

Salut,
Lorsque l'on a une fonction allant de l'ensemble E dans l'ensemble F (absolument quelconque tout les deux), on dit qu'elle est bijective lorsque tout Y de F est l'image d'un et un seul élément de E.
Au niveau calculs, ça correspond à choisir un Y quelconque, mais fixé dans F puis à résoudre l'équation (d'inconnue X) f(X)=Y. Pour que f soit bijective, il faut qu'il y ait systématiquement une et une seule solution.

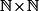
Dans le cas de ta fonction où, à priori (tu n'as pas précisé), l'ensemble de départ est (c'est à dire des couples d'entier) et l'ensemble d'arrivé est , il faut donc considérer un entier naturel fixé puis chercher tout les couples d'entiers naturels tels que . Si ta fonction est effectivement bijective, alors tu doit systématiquement (i.e. quelque soit le choisi) trouver qu'il y a un et un seul couple (m,n) solution.

Sauf que là, si on prend effectivement , ça ne va pas marcher du tout vu que pour , l'équation dc(m,n)=0 n'a pas de solutions (et pour y=2 l'équation f(m,n)=2 a deux solutions (0,1) et (1,0)).
Donc je pense qu'il y a une erreur dans ta fonction et que c'est plutôt (ou alors c'est que je n'ai pas compris ce que tu voulais faire...)

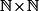
P.S. Si effectivement ce que tu cherche à construire c'est une bijection de dans , alors il me semble que ce n'est pas vraiment lié à ce qu'on appelle en généralement "l' argument diagonal de Cantor", mais c'est juste un problème de vocabulaire donc ça n'a pas vraiment d'importance.

[jankyjack]

oui effectivement c'est un m au lieu de 1.

et je n'ai pas precisé l'ensemble de depart parce que bêtement je me suis dit que quand o dit Cantor on dit ensemble N

mais sinon c'est effectivemnt aussi de N x N vers N

[URemery]

Bonjour,

La diagonale de Cantor c'est pas ça du tout désolé !

[jankyjack]

je ne saurai contredire les mathématiciens mais dans tous les cas parce que je ne me considere pas comme un mais si je ne m'abuse ceci plus haut est effectivement la fonction de la première methode de la diagonale cantor. En outre mon problème n'est pas de savoir qui a écrit la fonction ou pas mais mon problème ce demontrer que cette dernière est bijective et peu importe qu'elle vienne de cantor ou pas.

je vous remercie d'etre plus constructif

[URemery]

Je pense que vous confondez l'argument de la diagonale de Cantor qui a permit de démontrer que n'est pas dénombrable et la preuve que l'est.

En effet votre fonction permet bien de montrer que est en bijection avec et ce en montrant que est bijective, en appliquant la définition proposée par Ben314.

Par contre,

[jankyjack]

Effectivement dc(m,n) que tu as donné juste plus haut est different de cette somme. Parceque pour la diagonale on doit augmenter un + m pour que ce soit la fonction de la premiere methode de la diagonale de Cantor. Le truc est que je bloque au niveau de montrer que y=dc(m,n) existe et est unique et c'est justement là que j'ai besoin d'aide. Je connais deja les définitions de la bijectivité c'est dans l'application de ces definitions que je bute et j'ai besoin d'aide

[URemery]

Alors il me semble qu'il existe d'autre fonctions pour lesquelles la preuve est plus simple mais celle la est faisable quand même !
Le truc c'est qu'elle est basé sur une approche "graphique" on fait un tableau a double entrée, n et m, et dans la case (n, m) on met un nombre selon un schéma particulier, ce nombre correspond a . Ainsi pour la preuve on se base beaucoup sur ce tableau pour trouver les idées.

Pour montrer que on peut d'abord montrer qu'elle est injective,
ie
Ce qui donne en fait l'unicité.

Puis montrer qu'elle est surjective,
ie
Ce qui donne l'existence.

Il me semble que le plus dur est l'injectivité, j'essaye de retrouver dans mon coin l'argument adéquat.

[Ben314]

Dans un cas pareil, ça n'a pas vraiment d'intérêt de couper en deux et de montrer d'un coté l'injectivité et de l'autre la surjectivité : Vu que de toute façon il faut étudier l'équation dc(m,n)=y (pour la surjectivité), autant montrer directement qu'elle admet une unique solution plutôt que de montrer "à part" l'injectivité.

Et la preuve est relativement élémentaire :
Soit fixé. On cherche tels que .
On commence par chercher .
Comme , on a
Ce qui signifie que et, comme la suite commence à 0, est strictement croissante et tend vers +oo, il existe un unique entier naturel vérifiant cette inégalité (qu'on pourrait parfaitement calculer en résolvant l'inéquation du second degré (en ) , mais ça ne sert à rien)
Donc il n'y a pas le choix pour et il n'y a ensuite pas le choix pour vu qu'on doit prendre (qui est clairement un entier naturel) puis pas le choix pour vu qu'on doit prendre .
Il reste à vérifier que est bien un entier naturel, c'est à dire qu'il est positif ce qui revient à montrer que c'est à dire (vu la définition de ) que soit encore que ce qui est vrai en vertu de la deuxième inégalité qui a servi à définir .

Exemple : y=134 est supérieur ou égal à 120=15*16/2 et il est strictement plus petit que 136=16*17/2.
Donc s=15 puis m=134-120=14 et n=15-14=1 : 134=dc(1,14).

[URemery]

Ce qui signifie que et, comme la suite commence à 0, est strictement croissante et tend vers +oo, il existe un unique entier naturel vérifiant cette inégalité
.

Tu pourrais prouver ça stp ?

Ensuite pour ,
On a un discriminant et en notant les racines de ce polynome
et un tableau de signe donne comme ensemble de solutions. J'ai un peu de mal a voir ou se cache ce fameux seul solution de l’inéquation.

Merci d'éclairer ma lanterne

[URemery]

Ceci dit c'est vrai que la séparation injectivité, surjectivité est peut être superflue ...

Je suis plus confiant vis à vis de l'idée de chan79, il suffit de faire le "graphique" et on peut deviner l’antécédent, comme il le fait.

[Ben314]

A mon sens, c'est une évidence absolue, mais je peut essayer de le formuler différemment :
Si on note alors avec qui tend vers l'infini donc si tu prend un entier quelconque, il va forcément "s'intercaler" quelque part entre un certain et le suivant.
Et si tu veut une preuve "archi formelle", il te suffit de prendre l'ensemble des entiers naturels tels que : il est non vide vu que 0 est dedans et il est majoré vu que tend vers l'infini donc il admet un maximum et, évidement, n'est pas dans donc on a bien

Ensuite, concernant l'inéquation que tu as résolue (ce qui ne sert à rien pour la preuve), déjà tu t'es gouré : les solutions, c'est [x1,x2] et pas l'extérieur (il est clair que s²+s-2y est positif pour s "très grand") et ensuite, vu que ce que tu cherche, c'est le plus grand entier vérifiant l'inégalité en question (vu que ça ne doit pas marcher avec ), ça signifie que , c'est la partie entière de x2 :
Et l'unicité est de nouveau évidente : des entiers s tels que s soit dans [x1,x2], mais pas s+1, il ne risque pas d'y en avoir plusieurs : seul le plus grand entier de [x1,x2] possède cette propriété.
Mais je le redit, pour la preuve demandée, à part d'alourdir le discours, ça n'a pas d'intérêt de calculer explicitement s vu que l'objectif n'est pas la détermination de la bijection réciproque, mais uniquement de montrer que cette dernière existe.

Sinon, effectivement, de faire le graphique est évidement (et de loin) la façon la plus simple de se convaincre de la bijectivité de la fonction en question. Mais je pensait que jankyjack voulais une preuve "calculatoire" (on verra ce qu'il en dit...)

[chan79]

salut
L'antécédent de N est un peu pénible à expliciter
on arrive au couple:
avec
E=partie entière
pour N=31
k=E(7.38....)=7
m=31-28=3
n=-31+28+7=4
(m,n)=(3,4)


N=134
k=15
m=134-120=14
n=-134+120+15=1
(m,n)=(14,1)

[chan79]

un essai pour l'injectivité

On suppose que
Premier cas:
et sont alors différents et on a

Second cas: On suppose que (si l'écart entre et est plus grand que 1, on fait plusieurs étapes)

en effet, en développant et en réduisant au même dénominateur, on voit que l'inégalité équivaut à

donc

****************************************************
On peut démontrer la surjectivité par récurrence
on suppose que N a un antécédent (m,n)
N=(m+n)(m+n+1)/2+m
si n différent de 0, on a
N+1=((m+1)+(n-1))((m+1)+(n-1)+1)/2+(m+1)
donc N+1 a comme antécédent (m+1,n-1)
si n=0
N=m(m+1)/2+m
N+1=m(m+1)/2+(m+1)
N+1=(m+1)(m/2+1)=(m+1)(m+2)/2=(0+(m+1))(0+(m+1)+1)/2+0
donc N+1 a comme antécédent (0,m+1)
Pour l'initialisation 0=f(0,0)