L‘aire d‘un triangle (1ère S )

[galimatour]

Je m‘etait Trompé de catégorie!!
Bonsoir pouvez vous m‘aider , depuis hier j‘arrive pas à faire cette exercice!

[capitaine nuggets]

Salut !

Déjà puisque les points et dépendent de , l'aire du triangle sera une fonction de .
L'aire du triangle est égale à (on revient à des formules vues au collège).
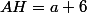
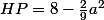
Montre qu'alors et , l'aire du triangle sera alors égale à . En développant, puis réduisant, tu devrais obtenir quelque chose de la forme , où , , et sont quatre réels à préciser. Pour trouver son éventuel maximum, tu dois étudier les variations de la fonction sur

Si je n'ai pas fait d'erreurs, tu devrais trouver un maximum égal à en .

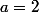
[galimatour]

Merciii beaucoup j’avais essayé de le faire hier et je suis à peut près tombé sur un truc de ce genre mais j’ai du galérer donc la je vais étudier le signe ! Encore merci