Bonjour,
Me voila bloqué sur un exercice d'un dm de maths à rendre pour dans quelque jours. Voici l'énoncé de l'exercice:
1) Soit deux points A et B tels que AB=6
a) Déterminer l'ensemble D des points M tels que (vecteurs) AM . AB= 12
b) Déterminer l'ensemble C des points M tels que: (vecteurs) AM . BM =-5
2) Soit ABC un triangle et I le milier du segment [BC].
a) Déterminer l'ensemble (E) des points M vérifiant: (vecteurs) MA . (MB+MC) = 0.
Aide: on pourra introduire le point I.
J'ai répondu à la première question en utilisant le projeté orthogonal de M sur AB et j'ai trouvé que l'ensemble correspondait à une droite perpendiculaire à AB passant par H (projeté de M) à 2 de A puisque les vecteurs AH et AB sont colinéaires et de même sens.
Je suis bloqué à les questions petit b... Que dois-je utiliser?
Et pour la question 2, j'ai essayé de développer l'expression en (vecteurs) MA . MB + MA . MC =0 et d'utiliser un théorème de la médiane mais je pense que ce n'est pas cela...
Merci d'avance de me guider.
Dm 1ère Spé maths (prduits scalaires)
13 messages
- Page 1 sur 1
Re: Dm 1ère Spé maths (prduits scalaires)
Bonjour,
Avec I milieu de [BC], pouvez-vous exprimer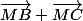 en fonction de
en fonction de 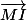 ?
?
Avec I milieu de [BC], pouvez-vous exprimer
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Dm 1ère Spé maths (prduits scalaires)
1b)
AM . BM =-5
Soit I le milieu de [AB] :
(AI + IM) . (BI + IM) = -5
On développe, on simplifie ... On arrive à IM^2 = 4
Ok ?
Si tu n'y arrives pas dis le.
AM . BM =-5
Soit I le milieu de [AB] :
(AI + IM) . (BI + IM) = -5
On développe, on simplifie ... On arrive à IM^2 = 4
Ok ?
Si tu n'y arrives pas dis le.
Re: Dm 1ère Spé maths (prduits scalaires)
hdci a écrit:Bonjour,
Avec I milieu de [BC], pouvez-vous exprimeren fonction de
?
(vecteurs) MB+MC=MI+IB+MI+IC
Re: Dm 1ère Spé maths (prduits scalaires)
titine a écrit:1b)
AM . BM =-5
Soit I le milieu de [AB] :
(AI + IM) . (BI + IM) = -5
On développe, on simplifie ... On arrive à IM^2 = 4
Ok ?
Si tu n'y arrives pas dis le.
(AI+IM) . (BI+IM) = -5 donne AI BI + AI . IM + IM . BI + IM . IM =-5
OU AI. -AI + AI . IM + IM . -AI +IM² =-5
-AI² + IM² =-5
IM² = AI² -5
IM= 9-5
IM= 4
C'est bien cela?
Si oui merci de votre aide.
Re: Dm 1ère Spé maths (prduits scalaires)
C'est IM²= 4 à la fin j'ai oublié de mettre le carré sur le deux dernières lignes.
Re: Dm 1ère Spé maths (prduits scalaires)
Concernant la question 2 a) J'ai essayé la même méthode. Pouvez-vous me dire ce que vous en pensez s'il vous plaît?
MA . (MB + MC) = 0
(MI + IA) . [(MI + IB) + (MI - IB) = 0
(MI + IA) . (MI + IB + MI -IB) = 0
(MI + IA) . 2MI =0
2MI² + 2MI . IA = 0
MI² + MI . IA = 0
MI²= - MI. IA MI=IA
L'ensemble C des points M vérifiant MA . (MB + MC) = 0 est un cercle de centre I et de diamètre CB.
MA . (MB + MC) = 0
(MI + IA) . [(MI + IB) + (MI - IB) = 0
(MI + IA) . (MI + IB + MI -IB) = 0
(MI + IA) . 2MI =0
2MI² + 2MI . IA = 0
MI² + MI . IA = 0
MI²= - MI. IA MI=IA
L'ensemble C des points M vérifiant MA . (MB + MC) = 0 est un cercle de centre I et de diamètre CB.
Re: Dm 1ère Spé maths (prduits scalaires)
MaxEsT a écrit:Concernant la question 2 a) J'ai essayé la même méthode. Pouvez-vous me dire ce que vous en pensez s'il vous plaît?
MaxEsT a écrit:L'ensemble C des points M vérifiant MA . (MB + MC) = 0 est un cercle de centre I et de diamètre CB.
Ce qui est gênant, c'est qu'il n'y a plus le point A. Le résultat peut-il vraiment être indépendant de A... ?
Dans ma proposition
hdci a écrit:Avec I milieu de [BC], pouvez-vous exprimeren fonction de
?
Il faut penser à un parallélogramme. I est le milieu de [BC], donc c'est le milieu de [MD] où D est tel que MBDC est un parallélogramme.
Donc à nouveau, pouvez-vous exprimer
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Dm 1ère Spé maths (prduits scalaires)
Je ne sais pas... Ce qui me gêne c'est que dans les deux questions on n'utilise pas les éléments vus dans le cours...
Re: Dm 1ère Spé maths (prduits scalaires)
Peut-être, mais vous avez forcément vu en seconde (encore que, avec le confinement...) que
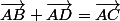
est équivalent à "ABCD est un parallélogramme (éventuellement aplati").
Dans un parallélogramme, les diagonales se coupent en...
Donc si I est le milieu du parallélogramme ABCD, alors
Faites une figure vous comprendrez.
Si ce que vous dites par "utiliser le cours", c'est caractériser un cercle par un produit scalaire, quand vous aurez fait tout cela vous verrez votre cercle (mais ce n'est pas de diamètre [BC])
est équivalent à "ABCD est un parallélogramme (éventuellement aplati").
Dans un parallélogramme, les diagonales se coupent en...
Donc si I est le milieu du parallélogramme ABCD, alors
Faites une figure vous comprendrez.
Si ce que vous dites par "utiliser le cours", c'est caractériser un cercle par un produit scalaire, quand vous aurez fait tout cela vous verrez votre cercle (mais ce n'est pas de diamètre [BC])
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Dm 1ère Spé maths (prduits scalaires)
hdci a écrit:Peut-être, mais vous avez forcément vu en seconde (encore que, avec le confinement...) que
est équivalent à "ABCD est un parallélogramme (éventuellement aplati").
Dans un parallélogramme, les diagonales se coupent en...
Donc si I est le milieu du parallélogramme ABCD, alors
Faites une figure vous comprendrez.
Si ce que vous dites par "utiliser le cours", c'est caractériser un cercle par un produit scalaire, quand vous aurez fait tout cela vous verrez votre cercle (mais ce n'est pas de diamètre [BC])
J'obtiens bien mon parallélogramme mais je ne vois pas en quoi I est le milieu de celui-ci. Oui les diagonales se coupent en leur milieu mais je ne vois pas quoi faire de ce que j'obtiens...
Oui effectivement je m'étais trompé dans ma conclusion mais dans mon résultat précédent mon cercle n'était pas de diamètre [BC], seulement de rayon [AI]. La solution n'était pas correcte?
Re: Dm 1ère Spé maths (prduits scalaires)
Avec [AI] c'est correct.
Définition d'un parallélogramme : c'est un quadrilatère dont les diagonales ont le même milieu.
Comme I est le milieu de [BC] c'est donc le milieu de [MD]
Donc
Comme on obtient
on obtient
=0\Leftrightarrow \vec{MA}\cdot\vec{MI}=0)
Et ceci est exactement la caractérisation du cercle de diamètre [AI]
Définition d'un parallélogramme : c'est un quadrilatère dont les diagonales ont le même milieu.
Comme I est le milieu de [BC] c'est donc le milieu de [MD]
Donc
Comme
Et ceci est exactement la caractérisation du cercle de diamètre [AI]
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
