Une partie dense dans les réelles !?
Olympiades mathématiques, énigmes et défis
-
Gathart
- Membre Naturel
- Messages: 20
- Enregistré le: 25 Sep 2012, 18:05
-
 par Gathart » 30 Sep 2012, 13:12
par Gathart » 30 Sep 2012, 13:12
J'ai un petit défi pour les mordus de problème ouvert que vous êtes !
Au cours de la préparation d'une leçon sur les sous-groupes additifs de

, je me suis demandé est-ce que
, n\in\mathbb{N}\})
est dense dans

? (Le problème a été posté il y a quelque temps dans une rubrique à l'ENS Cachan d'après mes sources)
Bon, on a déjà des éléments de réponse :
Pour
\in\mathbb{R}^2)

est dense dans

si et seulement si

D'où,
)
dense dans
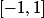
Pour
\in(\mathbb{R}_+^*)^2)

dense dans

si et seulement si

D'où,
)
dense dans

Mais qu'en est-il de
, n\in\mathbb{N} \})
? dense...ou pas ?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 30 Sep 2012, 14:31
par Luc » 30 Sep 2012, 14:31
Salut,
question intéressante!
est-ce que tu pourrais détailler le passage de

est dense dans

si et seulement si

à
)
dense dans
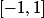
?
-
Gathart
- Membre Naturel
- Messages: 20
- Enregistré le: 25 Sep 2012, 18:05
-
 par Gathart » 30 Sep 2012, 14:42
par Gathart » 30 Sep 2012, 14:42
Voilivoilou ^^
\begin{Proposition}
 , \ n\in\mathbb{Z}\}$)
est dense dans

.
\end{Proposition}
\begin{Preuve}
Montrons que
$)
dense dans

.
Par

-périodicité
=\cos(\mathbb{Z}))
.
On a

dense dans
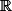
.
L'application cosinus est continue et surjective. Montrons que si

dense dans
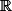
alors
$)
dense dans
=[-1,1]$)
.
Montrons que

avec
\cap O \neq \emptyset$)
.
\cap O)=f^{-1}(f(D))\cap f^{-1}(O) \supset D\cap D\cap f^{-1}(0))

dense dans
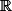
, on a que
\in\mathcal{T}_{\mathbb{R}}$)
(car
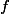
continue) et que
 \neq \emptyset$)
(car
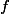
surjective). Donc
\neq \emptyset$)
,
\cap O))=f(D)\cap O$)
(par surjectivité).\\
Donc
=\cos(\mathbb{Z}))
est dense dans

.
\end{Preuve}
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 04 Oct 2012, 12:36
par Judoboy » 04 Oct 2012, 12:36
Un petit coup de main ? Je vois pas là.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Oct 2012, 13:01
par Nightmare » 04 Oct 2012, 13:01
Ne cherchez pas trop longtemps (sauf si vous êtes vraiment motivés), le problème est encore irrésolu par la communauté des mathématiciens à l'heure actuelle.
-
Gathart
- Membre Naturel
- Messages: 20
- Enregistré le: 25 Sep 2012, 18:05
-
 par Gathart » 04 Oct 2012, 23:18
par Gathart » 04 Oct 2012, 23:18
Bon, d'après JP Marco ce n'est pas bien compliqué XD !
Bon je n'ai pas de réponse évidemment mais j'ai des éléments intéressants.
L'approche diophantienne
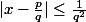
Continuer sur cette piste on peut obtenir des choses intéressantes malgré cela je n'aboutit à rien avec mes suites, d'où la seconde chose : construction d'une sous-suite de sous-suite en utilisant correctement l'approche diophantienne. Bon j'en suis à ce point là.
Normalement, une petite correction Lundi ^^
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Oct 2012, 23:22
par Nightmare » 04 Oct 2012, 23:22
Gathart a écrit:Bon, d'après JP Marco ce n'est pas bien compliqué XD !
Je crois qu'il a pas dû bien comprendre la question ^^
Peut être que le problème a été résolu récemment, mais je me rappelle en avoir discuté l'année dernière sur ce forum et l'on avait conclu après recherches sur internet que le problème était encore ouvert.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 05 Oct 2012, 03:09
par Doraki » 05 Oct 2012, 03:09
Je ne me souviens pas avoir vu ce problème sur le forum, mais je suis du même avis.
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 05 Oct 2012, 10:55
par Judoboy » 05 Oct 2012, 10:55
Nightmare a écrit:Ne cherchez pas trop longtemps (sauf si vous êtes vraiment motivés), le problème est encore irrésolu par la communauté des mathématiciens à l'heure actuelle.
Ca me rassure

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités