RacInès réelles d un polynôme sur C
19 messages
- Page 1 sur 1
RacInès réelles d un polynôme sur C
Bonjour
Je sèche sur le problème suivant : soit un polynôme de degré n P (z) a coefficients dans C et dont le coefficient de degré n est égal à 1. Si P admet n racines réelles alors Q (z)=P (z+ia)+P (z-ia) a n racines réelles quelque soit a appartenant à R.
Les degrés 2 et 3 sont assez faciles à démontrer et une récurrence semble appropriée mais je ne suis pas arrivé au bout.
Je sèche sur le problème suivant : soit un polynôme de degré n P (z) a coefficients dans C et dont le coefficient de degré n est égal à 1. Si P admet n racines réelles alors Q (z)=P (z+ia)+P (z-ia) a n racines réelles quelque soit a appartenant à R.
Les degrés 2 et 3 sont assez faciles à démontrer et une récurrence semble appropriée mais je ne suis pas arrivé au bout.
Re: RacInès réelles d un polynôme sur C
En grattouillant à droite à gauche, je suis tombé là dessus et je fait remonter vu que
- ça me semble intéressant et pas trivial.
- y'a pas la réponse.
- et que j'ai pas la réponse pour le moment...
P.S. Y'a éventuellement une ambiguïté concernant les "n racines réelles" : sont elles distinctes ou pas ?
Mais comme je sais pas trop par quel bout m'y prendre, aussi bien ça n'a pas d'importance (i.e. on peut les supposer non distinctes mais comptées avec leur ordre de multiplicité).
- ça me semble intéressant et pas trivial.
- y'a pas la réponse.
- et que j'ai pas la réponse pour le moment...
P.S. Y'a éventuellement une ambiguïté concernant les "n racines réelles" : sont elles distinctes ou pas ?
Mais comme je sais pas trop par quel bout m'y prendre, aussi bien ça n'a pas d'importance (i.e. on peut les supposer non distinctes mais comptées avec leur ordre de multiplicité).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: RacInès réelles d un polynôme sur C
salut
si le polynome P de degré n à coefficients dans C et de coefficient dominant 1 admet n racines réelles alors il me semble que P est à coefficients réels, non ?
puisqu'alors P s'écrit = \prod_1^n (z - r_i)) où les
où les 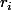 sont des réels (éventuellement confondus)
sont des réels (éventuellement confondus)


si le polynome P de degré n à coefficients dans C et de coefficient dominant 1 admet n racines réelles alors il me semble que P est à coefficients réels, non ?
puisqu'alors P s'écrit


Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: RacInès réelles d un polynôme sur C
Oui, ça me semble bien ça : P est évidement à coeff. réels et l'énoncé est un peu "biscornu" de ce coté là.
Je suppose que l'évocation des complexes au début de l'énoncé est juste là pour signaler que le i que apparait ensuite, c'est le i des complexes.
Tu montre aussi très facilement que le polynôme Q est lui aussi à coefficient réels, mais j'ai pas trouvé comment montrer qu'il est scindé dans R.
Je suppose que l'évocation des complexes au début de l'énoncé est juste là pour signaler que le i que apparait ensuite, c'est le i des complexes.
Tu montre aussi très facilement que le polynôme Q est lui aussi à coefficient réels, mais j'ai pas trouvé comment montrer qu'il est scindé dans R.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: RacInès réelles d un polynôme sur C
C'est le genre de truc dont je suis quasi-sûr d'avoir déjà vu quelque part.
Re: RacInès réelles d un polynôme sur C
ha d'accord ... j'ai eu peur ...
oui effectivement ensuite Q est donc réel
bon moi non plus je ne vois pas plus loin ... mais ça ne m'étonne pas ...
oui effectivement ensuite Q est donc réel
bon moi non plus je ne vois pas plus loin ... mais ça ne m'étonne pas ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: RacInès réelles d un polynôme sur C
Je sais pas si je l'ai pas déjà vu quelque part aussi...
Sinon, il me semble qu'une autre façon d'énoncer le problème, c'est de considérer l'ensemble E des complexes z tels que P(z) soit imaginaire pur et de montrer que l'intersection de E avec toute droite parallèle à l'axe réel contient n éléments (dans le cas où P est à racines distinctes et qu'on veut montrer que Q aussi).
Et là, ça sent assez fort le théorème d'inversion locale pour "suivre" les courbes constituant E : j'ai l'impression qu'on montre relativement facilement qu'elles ne se croisent pas et qu'elles n'ont jamais de tangentes horizontales ce qui, intuitivement parlant, semble suffire à démontrer le résultat...
Sinon, il me semble qu'une autre façon d'énoncer le problème, c'est de considérer l'ensemble E des complexes z tels que P(z) soit imaginaire pur et de montrer que l'intersection de E avec toute droite parallèle à l'axe réel contient n éléments (dans le cas où P est à racines distinctes et qu'on veut montrer que Q aussi).
Et là, ça sent assez fort le théorème d'inversion locale pour "suivre" les courbes constituant E : j'ai l'impression qu'on montre relativement facilement qu'elles ne se croisent pas et qu'elles n'ont jamais de tangentes horizontales ce qui, intuitivement parlant, semble suffire à démontrer le résultat...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: RacInès réelles d un polynôme sur C
Elles devraient pouvoir se croiser si elles passent par un endroit où P' s'annule. Mais comme on connaît l'angle qu'elles font, à moins que y'en ait une qui soit horizontale, y'a pas de problème.
Re: RacInès réelles d un polynôme sur C
Oui, mais vu que P est à racine réelles (supposées distinctes), les racines de P' sont aussi toutes réelles et distinctes de celles de P. Donc, P' ne s'annule pas sur E.Doraki a écrit:Elles devraient pouvoir se croiser si elles passent par un endroit où P' s'annule.
D'un autre coté, tu as aussi raison dans le sens que, même si P' s'annulait sur E, on contrôlerais facilement la multiplicité de l'intersection et les angles des tangentes. Et ça doit être utile si on s'intéresse au cas où P admet des racines multiples.
P.S. Si on regarde le cas "le pire" concernant les racines multiples, c'est P(X)=X^n et dans ce cas, le polynôme Q_a est bien scindé dans R quelque soit la valeur de a.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: RacInès réelles d un polynôme sur C
ah ben oui tiens les racines de P' sont toutes réelles j'avais oublié ^^'
Ben commes les courbes ne se croisent pas et sont disjointes et vont à l'infini,
et comme pour chaque ligne horizontale il y a au plus n intersections,
elles ne peuvent pas se mettre à redescendre sinon y'aurait une ligne avec n+2 (ou pire) intersections.
Ca doit être pas facile à formaliser proprement.
Ben commes les courbes ne se croisent pas et sont disjointes et vont à l'infini,
et comme pour chaque ligne horizontale il y a au plus n intersections,
elles ne peuvent pas se mettre à redescendre sinon y'aurait une ligne avec n+2 (ou pire) intersections.
Ca doit être pas facile à formaliser proprement.
Re: RacInès réelles d un polynôme sur C
J'ai l'impression que, sur le principe, E pourrait éventuellement contenir deux espèces de paraboles disjointes, l'une tournée "vers le bas", l'autre "vers le haut" et le sommet de celle "vers le haut" qui soit au dessus de celui "vers le bas". Sauf erreur, ça serait le cas avec (a\!-\!2)) .
.
C'est pour éviter ce cas qu'il me semblait utile de montrer que les courbes formant E n'ont jamais de tangente horizontale.
Sinon, je suis d'accord avec le fait que ça doit pas être super facile à formuler correctement.
Mais je pense que c'est jouable à coup de topo : soit Z l'ensemble des A tels que, quelque soit a dans [0,A] le polynôme Q_a soit scindé puis, si Z est différent de R+, soit A0 le sup de Z.....
C'est pour éviter ce cas qu'il me semblait utile de montrer que les courbes formant E n'ont jamais de tangente horizontale.
Sinon, je suis d'accord avec le fait que ça doit pas être super facile à formuler correctement.
Mais je pense que c'est jouable à coup de topo : soit Z l'ensemble des A tels que, quelque soit a dans [0,A] le polynôme Q_a soit scindé puis, si Z est différent de R+, soit A0 le sup de Z.....
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: RacInès réelles d un polynôme sur C
Non, les différents 0 de P ne peuvent pas être sur les mêmes composantes connexes, parceque avec le théorème des fonctions implicites, quand tu te balades le long de E, Im(P(z)) va être monotone. Donc passer deux fois (ou plus) par l'axe des réels donc par 0, ça va pas être possible.
Re: RacInès réelles d un polynôme sur C
Je me suis mal exprimé : lorsque je parlais du "théorème d'inversion locale", j'avais déjà en tête que la différentielle de phi:(a,x)->Q_a(x) est non nulle lorsque (a,x) est dans E (sauf éventuellement si a=0 et x est une racine multiple de P). Donc localement, E est bien formé de courbes (et il n'y a pas d'intersection possibles).
Mais par contre, j'ai pas réussi à montrer qu'on peut partout paramétrer par du a->une_racine_de_Q_a, c'est à dire que d.phi/dx, est non nul sur E, c'est à dire en fait que Q_a est sans racines double.
Mais par contre, j'ai pas réussi à montrer qu'on peut partout paramétrer par du a->une_racine_de_Q_a, c'est à dire que d.phi/dx, est non nul sur E, c'est à dire en fait que Q_a est sans racines double.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: RacInès réelles d un polynôme sur C
Si P a n racines distinctes,
pour chaque racine ρ, on a une immersion f : R -> C tq f(0) = ρ et P(f(y)) = iy grâce au théorème des fonctions implicites et le fait que les racines de P' sont ailleurs sur l'axe des réels.
Les images de chaque f sont deux à deux disjointes parceque f est entièrement déterminé par une seule de ses valeurs.
Et comme P ~ x^n en l'infini, |Im(f(y))| tend vers l'infini quand |y| tend vers l'infini. De plus comme f ne peut passer qu'une seule fois par l'axe des réels, y -> Im(f(y)) doit être surjective (de R dans R), et donc pour tout a, Qa doit avoir au moins n racines distinctes.
Mais comme Qa est un polynôme de degré n, toutes ces racines sont simples et il n'y en a pas d'autre,
Et donc dphi/dx ne peut pas s'annuler sur E et au passage, les fonctions y -> Im(f(y)) sont des difféomorphismes de R dans R.
---
Après on peut probablement en déduire le cas où P a des racines multiples par un argument de densité
pour chaque racine ρ, on a une immersion f : R -> C tq f(0) = ρ et P(f(y)) = iy grâce au théorème des fonctions implicites et le fait que les racines de P' sont ailleurs sur l'axe des réels.
Les images de chaque f sont deux à deux disjointes parceque f est entièrement déterminé par une seule de ses valeurs.
Et comme P ~ x^n en l'infini, |Im(f(y))| tend vers l'infini quand |y| tend vers l'infini. De plus comme f ne peut passer qu'une seule fois par l'axe des réels, y -> Im(f(y)) doit être surjective (de R dans R), et donc pour tout a, Qa doit avoir au moins n racines distinctes.
Mais comme Qa est un polynôme de degré n, toutes ces racines sont simples et il n'y en a pas d'autre,
Et donc dphi/dx ne peut pas s'annuler sur E et au passage, les fonctions y -> Im(f(y)) sont des difféomorphismes de R dans R.
---
Après on peut probablement en déduire le cas où P a des racines multiples par un argument de densité
Modifié en dernier par Doraki le 12 Déc 2016, 15:49, modifié 1 fois.
Re: RacInès réelles d un polynôme sur C
Ca roule, sauf un truc où je te suis pas trop (mais qui ne change rien à la preuve) :
Tu écrit que les fonctions y -> Im(f(y)) sont des difféo. alors qu'à mon sens, les argument au dessus montrent uniquement que ce sont des homéo., non ? (ou alors j'ai raté quelque chose...)
Je pense à ça parce que, si ta fonction f on l'écrit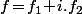 (avec
(avec  un homéo. de R->R) alors les fonctions g que je cherchais vérifiant P(g(a)+ia) dans iR pour tout a, en fait, c'est
un homéo. de R->R) alors les fonctions g que je cherchais vérifiant P(g(a)+ia) dans iR pour tout a, en fait, c'est 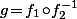 et, vu sous cet angle, pour que g soit dérivable, il faut effectivement que
et, vu sous cet angle, pour que g soit dérivable, il faut effectivement que  soit un difféo. et pas uniquement un homéo.
soit un difféo. et pas uniquement un homéo.
Tu écrit que les fonctions y -> Im(f(y)) sont des difféo. alors qu'à mon sens, les argument au dessus montrent uniquement que ce sont des homéo., non ? (ou alors j'ai raté quelque chose...)
Je pense à ça parce que, si ta fonction f on l'écrit
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: RacInès réelles d un polynôme sur C
En différentiant P(f(y)) = iy on obtient
P'(f(y)) * df/dy = i
donc df/dy = i / P'(f(y))
si tu écris P'(f(y)) = a+ib (je devrais dire a(y) et b(y) mais flemme),
tu as df/dy = i/(a+ib) = (b+ia)/(a²+b²), et donc en posant f(y) = X+iY,
dY/dy = a/(a²+b²).
D'un autre coté, si QY : x -> P(x+iY) + P(x-iY) = 2Re(P(x+iY)),
on a QY(X) = 2Re(P(f(z))) = 2Re(iy) = 0,
et a QY'(x) = 2Re(P'(x+iY)) (Re est R-linéaire), et donc QY'(X) = 2Re(P'(f(y))) = 2Re(a+ib) = 2a
Donc dY/dy = 0 <=> a=0 (P' est imaginaire pur en f(y)) <=> QY'(X) = 0 <=> QY a une racine (au moins) double en X
Comme on sait que les racines de QY sont toutes simples, ça implique que P' n'est jamais imaginaire pur sur E, et que dY/dy ne s'annule jamais, donc c'est un difféomorphisme.
---
D'ailleurs je conjecturerais bien que l'argument de P'(f(y)) est monotone quand y varie.
P'(f(y)) * df/dy = i
donc df/dy = i / P'(f(y))
si tu écris P'(f(y)) = a+ib (je devrais dire a(y) et b(y) mais flemme),
tu as df/dy = i/(a+ib) = (b+ia)/(a²+b²), et donc en posant f(y) = X+iY,
dY/dy = a/(a²+b²).
D'un autre coté, si QY : x -> P(x+iY) + P(x-iY) = 2Re(P(x+iY)),
on a QY(X) = 2Re(P(f(z))) = 2Re(iy) = 0,
et a QY'(x) = 2Re(P'(x+iY)) (Re est R-linéaire), et donc QY'(X) = 2Re(P'(f(y))) = 2Re(a+ib) = 2a
Donc dY/dy = 0 <=> a=0 (P' est imaginaire pur en f(y)) <=> QY'(X) = 0 <=> QY a une racine (au moins) double en X
Comme on sait que les racines de QY sont toutes simples, ça implique que P' n'est jamais imaginaire pur sur E, et que dY/dy ne s'annule jamais, donc c'est un difféomorphisme.
---
D'ailleurs je conjecturerais bien que l'argument de P'(f(y)) est monotone quand y varie.
Re: RacInès réelles d un polynôme sur C
Ca roule (et en plus, lors de mes pérégrinations pour essayer de montrer l'existence de g, j'avais bien vu cette série d'équivalence)
Si c'est bien le cas, lorsque n est impair, la fonction f associée à la racine "du milieu" serait telle que f'(0) et f'(+-oo) ait le même argument. Si l'argument était monotone, il serait constant et... ça m'étonnerais un peu...
Là, j'ai des doutes : pour toute les fonctions f, on a f'(0) imaginaire pur (i.e. les courbes partent perpendiculairement à l'axe des x) et je pense que, lorsque t->+-oo, le fait que P(X)~X^n fait que les f'(t) ont des arguments qui tendent vers des Pi/(2n)+k.Pi/n.Doraki a écrit:D'ailleurs je conjecturerais bien que l'argument de P'(f(y)) est monotone quand y varie.
Si c'est bien le cas, lorsque n est impair, la fonction f associée à la racine "du milieu" serait telle que f'(0) et f'(+-oo) ait le même argument. Si l'argument était monotone, il serait constant et... ça m'étonnerais un peu...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: RacInès réelles d un polynôme sur C
Une autre démarche, plus facile à saisir ..  On va généraliser un peu .
On va généraliser un peu .
Soit un polynôme dont toutes les racines
dont toutes les racines 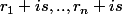 ont la même partie imaginaire :
ont la même partie imaginaire : =\prod_{k=1}^n(z- r_k-is)) . (
. (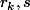 réels,
réels, 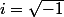 )
)
Soit le polynôme=P(z+ia)+tP(z-ia)) , non réduit à une constante,
, non réduit à une constante,
avec réel et
réel et  complexe tel que
complexe tel que 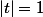 .
.
On va montrer que toutes les racines de ont la même partie imaginaire
ont la même partie imaginaire 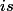 .
.
Si c'est trivial puisque les racines de
c'est trivial puisque les racines de  sont celles de
sont celles de  . On va supposer
. On va supposer 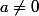 .
.
Soit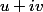 (
(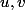 réels) une racine de
réels) une racine de  :
:
=0\Longrightarrow \prod_{k=1}^n(u+iv+ia- r_k-is)=-t\prod_{k=1}^n(u+iv-ia- r_k-is)\Longrightarrow)
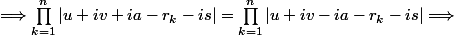
^2+(u- r_k)^2|=\prod_{k=1}^n((v-s-a)^2+(u- r_k)^2|)
Il s'ensuit^2=(v-s-a)^2) donc
donc 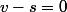 donc la même partie imaginaire
donc la même partie imaginaire 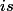 (q.e.d)
(q.e.d)
(J'avais déjà posté cette solution il y a qq années, mais je ne me rappelle plus où ..)

Soit un polynôme
Soit le polynôme
avec
On va montrer que toutes les racines de
Si
Soit
Il s'ensuit
(J'avais déjà posté cette solution il y a qq années, mais je ne me rappelle plus où ..)

19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
