Trigonométrie en or !
Olympiades mathématiques, énigmes et défis
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 18 Déc 2008, 22:16
par Zweig » 18 Déc 2008, 22:16
Salut,
Montrer que
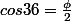
Enjoy !
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 18 Déc 2008, 22:18
par XENSECP » 18 Déc 2008, 22:18
C'est quoi phi ? ^^
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 18 Déc 2008, 22:19
par Zweig » 18 Déc 2008, 22:19
Le nombre d'or :
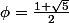
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 18 Déc 2008, 22:21
par XENSECP » 18 Déc 2008, 22:21
Of course ^^
Hum ça me dit qqch... mais le démontrer peut être pas :D Il faut repasser par des polynômes il me semble... la flemme :D
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 18 Déc 2008, 22:26
par Zweig » 18 Déc 2008, 22:26
En effet ... :id:
-
jeancam
- Membre Relatif
- Messages: 171
- Enregistré le: 07 Nov 2008, 21:54
-
 par jeancam » 18 Déc 2008, 22:42
par jeancam » 18 Déc 2008, 22:42
Zweig a écrit:En effet ... :id:
geometriquement avec un pentagone et pythagore çà devrai aussi marcher
polynomes mais de degres 2...

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 18 Déc 2008, 23:22
par nuage » 18 Déc 2008, 23:22
Salut,
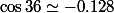
sauf erreur de ma part.
Ne voudrais tu pas parler de
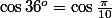
?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 19 Déc 2008, 14:43
par Zweig » 19 Déc 2008, 14:43
Ma calculatrice me donne cos 36 = 0.809, qui est bien égal à
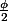
-
speedy
- Membre Relatif
- Messages: 170
- Enregistré le: 17 Nov 2007, 12:03
-
 par speedy » 19 Déc 2008, 15:19
par speedy » 19 Déc 2008, 15:19
Pour prouver ce que tu nous avance il faut faire une étoile .. :we:
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 19 Déc 2008, 18:47
par ThSQ » 19 Déc 2008, 18:47
nuage a écrit: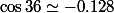
36 radians oui :hey:
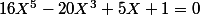
m'semble
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 19 Déc 2008, 19:29
par lapras » 19 Déc 2008, 19:29
Bonsoir,
pour éviter le polynome du 5eme degré :
=sin(\pi-\frac{2\pi}{5})=sin(\frac{3\pi}{5}))
or
= sin(2x)cos(x)+cos(2x)sin(x)=2cos(x)^2sin(x)+sin(x)(1-2sin(x)^2)=3sin(x)-4sin(x)^3)
et
=2sin(x)cos(x))
donc
(2cos(\frac{\pi}{5})+4sin(\frac{\pi}{5})^2-3)=0)
donc
+4sin(\frac{\pi}{5})^2-3=0=-4cos(\frac{\pi}{5})^2+ 2cos(\frac{\pi}{5})+1)
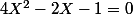
donc
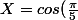 = \frac{1+\sqrt{5}}{4}=\frac{\phi}{2})
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 20 Déc 2008, 10:04
par Babe » 20 Déc 2008, 10:04
bonjour,
comment passer vous de cos36 au polynome ?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 20 Déc 2008, 12:22
par ThSQ » 20 Déc 2008, 12:22
Babe a écrit:bonjour,
comment passez vous de cos36 au polynome ?
Moivre !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités