Un petit exercice sympa !
Montrer les identités suivantes :
i)
ii)
Trigonométrie
3 messages
- Page 1 sur 1
Trigonométrie
par Zweig » 21 Jan 2009, 14:58
Salut,
Un petit exercice sympa !
Montrer les identités suivantes :
i)\pi}{n}=\frac{n}{2^{n-1}})
ii)\pi}{2n}=\frac{1}{2^{n-1}})
Un petit exercice sympa !
Montrer les identités suivantes :
i)
ii)
par lapras » 21 Jan 2009, 16:53
Salut,
c'est un exo d'olympiade ?
Parce que c'est assez calculatoire...
Je réécrit l'équation demandée :
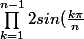 = n)
Maintenant, on remarque que :
 = \frac{e^{\frac{i*k\pi}{n}} - e^{-\frac{i*k\pi}{n}}}{i})
Or on sait calculer}{n}} - 1))
puisque les }{n}})
sont les racines n-iemes de l'unités
donc
}{n}} - 1) = (-1)^{n-1}\prod_{k=1}^{n-1} (1-e^{\frac{i*(2k\pi)}{n}}) = (-1)^{n-1}n)
...
Or
}{n}} - 1}{e^{-\frac{ik\pi}{n}})
On calcule et on a le résultat voulu.
c'est un exo d'olympiade ?
Parce que c'est assez calculatoire...
Je réécrit l'équation demandée :
Maintenant, on remarque que :
Or on sait calculer
donc
Or
On calcule et on a le résultat voulu.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :