Suite harmonique
Olympiades mathématiques, énigmes et défis
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 23 Juin 2006, 14:20
par yos » 23 Juin 2006, 14:20
Bonjour. voilà une proposition d'exo.
Soit
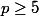
un nombre premier.
Démontrer que la fraction

a un numérateur multiple de
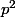
.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 23 Juin 2006, 16:46
par aviateurpilot » 23 Juin 2006, 16:46
k})
donc il existe B tel que
!^2})
avec B divisible par p
donc le numérateur de A (ou
=1)
)est
!^2)})
donc
N est divisible par p car
!^2))
ne divise pas p
si numerateur de A est divisible par p alors le numerteur de
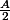
l'est aussi
il faut maintenant que je montre que le numerateur de }) est un multiple de p
est un multiple de p
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 23 Juin 2006, 17:55
par yos » 23 Juin 2006, 17:55
Bien vu.
On peut aussi se placer dans le corps Z/pZ. Les éléments 1,2,...,p-1 ont pour inverse 1,2,...,p-1 (dans le désordre), et donc
Sp= 1+1/2+...+1/(p-1)=1+2+...+(p-1)=p(p-1)/2=0.
Mais là aussi, on n'a pas fini.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 05 Juil 2006, 11:04
par yos » 05 Juil 2006, 11:04
Toujours pas de réponse pour p²...
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Juil 2006, 15:32
par yos » 10 Juil 2006, 15:32
On considère le polynôme
)
défini par :
=(X-1)(X-2)...(X-p+1))
.
On l'écrit :
=X^{p-1}+a_{p-2}X^{p-2}+...+a_2X^2+a_1X+a_0)
.
Puisque
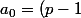!)
le calcul de
)
avec les deux expressions donne :
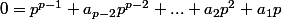
, (1)
Les coefficients

pour

sont tous multiples de

(comment ça vous ne voyez pas pourquoi?!), de sorte que (1) nous donne

.
!})
n'est autre que la fraction
)
. La simplifier n'y changerait rien car (p-1)! est étranger à p.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 10 Juil 2006, 16:35
par aviateurpilot » 10 Juil 2006, 16:35
j'ai aimé cette methode :we:
soit l'ensemble E={

}
est
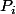
=l'ensemble des produit des elements des parties de E à i elements

est la somme des element de
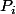
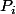
={

}
!}=\bigsum_{k=1}^{C_{p-1}^{i}}\frac{1}{b_{p-1-i}})
cas particulier:
pour i=1

={

}=E
!}=\bigsum_{k=1}^{p-1}\frac{1}{k})
et c'est ce que yos a dit.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Juil 2006, 21:03
par yos » 10 Juil 2006, 21:03
Je crois qu'il y a un bug dans ce que tu dis :
tu dois mettre

à la place de

, mais bon l'idée est là.
Par contre le fait que les

soient des multiples de p n'est pas trivial il me semble. Ce point est-il à détailler?
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 10 Juil 2006, 21:40
par aviateurpilot » 10 Juil 2006, 21:40
Je crois qu'il y a un bug dans ce que tu dis
c'ete ce que je voulais dire
mais j'ai pas vu cette petite faute
Par contre le fait que les

soient des multiples de p n'est pas trivial il me semble. Ce point est-il à détailler?
non. c'est facile
merci pour cette methode
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 13 Juil 2006, 15:49
par yos » 13 Juil 2006, 15:49
A noter que ce résultat porte le nom de théorème de Wolstenholme.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 13 Juil 2006, 15:52
par aviateurpilot » 13 Juil 2006, 15:52
théorème de Wolstenholme.
merci pour cette information :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités