Une série harmonique privée de son neuf ...

[Elerinna]

Déterminer la nature de la série obtenue en enlevant à la série harmonique tous les termes dont le dénominateur comporte au moins un neuf :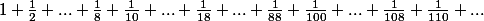 :zen:

[Matt_01]

Il suffit de compter le nombre d'entiers naturels à k chiffres qui ne contiennent pas de 9 : on a 8 choix pour le premier chiffre (on exclut 0) et 9 choix pour les autres, ce qui fait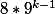
Or x possède k chiffres est équivalent à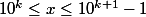
Au final notre somme est égal à :

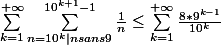qui converge en tant que somme géométrique.