Somme infinie de logarithmes
Olympiades mathématiques, énigmes et défis
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 04 Mar 2012, 17:33
par Zweig » 04 Mar 2012, 17:33
Salut,
Calculer
[CENTER]
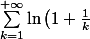\cdot \ln\left(\displaystyle 1 + \frac{1}{2k}\right)\cdot \ln\left(\displaystyle 1 + \frac{1}{2k+1}\right))
[/CENTER]
Bonne chance !
-
manoa
- Membre Relatif
- Messages: 343
- Enregistré le: 12 Oct 2011, 00:02
-
 par manoa » 04 Mar 2012, 18:05
par manoa » 04 Mar 2012, 18:05
Zweig a écrit:Salut,
Calculer
[CENTER]
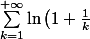\cdot \ln\left(\displaystyle 1 + \frac{1}{2k}\right)\cdot \ln\left(\displaystyle 1 + \frac{1}{2k+1}\right))
[/CENTER]
Bonne chance !
Bonsoir,
La notation signifie-elle la limite de la suite
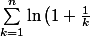\cdot \ln\left(\displaystyle 1 + \frac{1}{2k}\right)\cdot \ln\left(\displaystyle 1 + \frac{1}{2k+1}\right))
?
en fait il est faisable avec un bagage niveau TS ?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 04 Mar 2012, 18:22
par Zweig » 04 Mar 2012, 18:22
Exactement, on cherche à déterminer la limite de cette suite. Et oui, c'est faisable avec un bagage de T°S.
-
manoa
- Membre Relatif
- Messages: 343
- Enregistré le: 12 Oct 2011, 00:02
-
 par manoa » 04 Mar 2012, 21:40
par manoa » 04 Mar 2012, 21:40
Je cherche depuis toute à l'heure du côté des sommes télescopiques pour encadrer, mais ça avance pas :hum:
une piste ? :we:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 05 Mar 2012, 01:10
par Zweig » 05 Mar 2012, 01:10
Bien sûr !
On pose
 = \ln\,\left(\displaystyle 1+ \frac{1}{n}\right))
. Etablis une relation liant
)
à
)
et
)
. Ensuite trouve une fonction

vérifiant : [CENTER]
f(2n+1)f(2n) = \displaystyle \frac{g(n) - g(n+1)}{3})
[/CENTER]
Ton télescopage tant recherché en découle alors :lol3:
-
manoa
- Membre Relatif
- Messages: 343
- Enregistré le: 12 Oct 2011, 00:02
-
 par manoa » 05 Mar 2012, 15:30
par manoa » 05 Mar 2012, 15:30
Zweig a écrit:Bien sûr !
On pose
 = \ln\,\left(\displaystyle 1+ \frac{1}{n}\right))
. Etablis une relation liant
)
à
)
et
)
. Ensuite trouve une fonction

vérifiant : [CENTER]
f(2n+1)f(2n) = \displaystyle \frac{g(n) - g(n+1)}{3})
[/CENTER]
Ton télescopage tant recherché en découle alors :lol3:
Salut,
j'ai trouvé
=f(2n)+f(2n+1))
puis après calcul :
f(2n+1)f(2n) = f^3(n)-f^3(2n)-f^3(2n+1))
mais je ne vois pas vraiment le g vu qu'il n y a pas de relation récurrente entre ces termes.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 05 Mar 2012, 21:22
par Zweig » 05 Mar 2012, 21:22
manoa a écrit:Salut,
j'ai trouvé
=f(2n)+f(2n+1))
puis après calcul :
f(2n+1)f(2n) = f^3(n)-f^3(2n)-f^3(2n+1))
mais je ne vois pas vraiment le g vu qu'il n y a pas de relation récurrente entre ces termes.
Ce que tu as fait est bon. Pour trouver

, remarque que
 = \displaystyle \sum^{2n-1}_{k=n} f^3(k) - \displaystyle \sum^{2n-1}_{k=n+1} f^3(k))
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 05 Mar 2012, 21:51
par Jota Be » 05 Mar 2012, 21:51
Zweig a écrit:Ce que tu as fait est bon. Pour trouver

, remarque que
 = \displaystyle \sum^{2n-1}_{k=n} f^3(k) - \displaystyle \sum^{2n-1}_{k=n+1} f^3(k))
Salut Zweig,
j'ai essayé ceci mais je n'arrive pas à trouver g(n) et g(n+1), bien que les sommes s'en rapprochent. Peut-on effectuer un changement de variables ?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 05 Mar 2012, 21:54
par Zweig » 05 Mar 2012, 21:54
Rajoute dans les deux membres -
)
et -
)
puis fais les "rentrer" dans l'une des sommes, tu devrais pouvoir alors déterminer g sans problème.
-
manoa
- Membre Relatif
- Messages: 343
- Enregistré le: 12 Oct 2011, 00:02
-
 par manoa » 05 Mar 2012, 22:56
par manoa » 05 Mar 2012, 22:56
Haa ! ça me donne
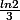
,
mais je ne suis pas sûr que la limite de
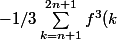)
vaut 0 c'est juste un sentiment, il faut l'encadrer c'est bien ça ?
En fait je me suis toujours demandé si
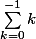
a un sens et qu'est ce qu'elle vaut .
joli problème :zen:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 05 Mar 2012, 23:03
par Zweig » 05 Mar 2012, 23:03
La limite de
 = \displaystyle \sum^{2n-1}_{k=n}f^3(k))
vaut 0 oui, tu utilise
\leq x)
.
Par contre c'est plutôt
}{3})
-
manoa
- Membre Relatif
- Messages: 343
- Enregistré le: 12 Oct 2011, 00:02
-
 par manoa » 05 Mar 2012, 23:12
par manoa » 05 Mar 2012, 23:12
Zweig a écrit:La limite de
 = \displaystyle \sum^{2n-1}_{k=n}f^3(k))
vaut 0 oui, tu utilise
\leq x)
.
Par contre c'est plutôt
}{3})
Ah oui c'est bien cela,merci !
sinon (hors sujet)
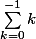
vaut 0 ?
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 05 Mar 2012, 23:17
par Jota Be » 05 Mar 2012, 23:17
Zweig a écrit:La limite de
 = \displaystyle \sum^{2n-1}_{k=n}f^3(k))
vaut 0 oui, tu utilise
\leq x)
.
Par contre c'est plutôt
}{3})
hmmm, je trouve
}-\sum_{k=n+1}^{2n+1} \ln^3{\left(1+\frac{1}{k}\right)}}{3})
.
ça me donne le même résultat mais est-ce juste ?
-
manoa
- Membre Relatif
- Messages: 343
- Enregistré le: 12 Oct 2011, 00:02
-
 par manoa » 06 Mar 2012, 00:12
par manoa » 06 Mar 2012, 00:12
Jota Be a écrit:hmmm, je trouve
}-\sum_{k=n+1}^{2n+1} \ln^3{\left(1+\frac{1}{k}\right)}}{3})
.
ça me donne le même résultat mais est-ce juste ?
Oui c'est juste :lol3:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 06 Mar 2012, 12:17
par Zweig » 06 Mar 2012, 12:17
manoa a écrit:Ah oui c'est bien cela,merci !
sinon (hors sujet)
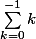
vaut 0 ?
Bah, ce serait plutôt
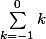
(le plus petit indice en bas), du coup ça ferait -1.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 06 Mar 2012, 12:18
par Zweig » 06 Mar 2012, 12:18
Jota Be a écrit:hmmm, je trouve
}-\sum_{k=n+1}^{2n+1} \ln^3{\left(1+\frac{1}{k}\right)}}{3})
.
ça me donne le même résultat mais est-ce juste ?
Oui, reste plus qu'à montrer que la limite de la somme vaut 0.
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 06 Mar 2012, 18:43
par Jota Be » 06 Mar 2012, 18:43
Zweig a écrit:Oui, reste plus qu'à montrer que la limite de la somme vaut 0.
Salut,
Je dirais
}=\lim\limits_{n\to\infty}\ln^3{ \left(1+ \frac{1}{n+1} \right)}+\ln^3{ \left(1+ \frac{1}{n+2} \right)}+...+\ln^3{\left(1+ \frac{1}{2n} \right)}+\ln^3{ \left(1+ \frac{1}{2n+1} \right)})
avec
}=\ln^3{(1)}=\ln{(1)}=0)
et
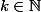
, alors
}=0)
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 06 Mar 2012, 19:23
par Doraki » 06 Mar 2012, 19:23
Non, c'est pas parceque les trucs sommés tendent vers 0 que la suite tend vers 0.
Là avec ton raisonnement tu es en train de dire que la suite 1, 1/2+1/2, 1/3+1/3+1/3, 1/4+1/4+1/4+1/4, ... tend vers 0
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 06 Mar 2012, 19:25
par Jota Be » 06 Mar 2012, 19:25
Doraki a écrit:Non, c'est pas parceque les trucs sommés tendent vers 0 que la suite tend vers 0.
Là avec ton raisonnement tu es en train de dire que la suite 1, 1/2+1/2, 1/3+1/3+1/3, 1/4+1/4+1/4+1/4, ... tend vers 0
Si n tend vers l'infini, on ne rencontre pas ce problème-là, si ?
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 06 Mar 2012, 19:26
par Jota Be » 06 Mar 2012, 19:26
Doraki a écrit:Non, c'est pas parceque les trucs sommés tendent vers 0 que la suite tend vers 0.
Là avec ton raisonnement tu es en train de dire que la suite 1, 1/2+1/2, 1/3+1/3+1/3, 1/4+1/4+1/4+1/4, ... tend vers 0
ok, je m'étais dit que ça ne devait pas être aussi simple. Je vais essayer une autre méthode
Tu parles de suite. Doit-on remarquer une suite géométrique ? J'avais pensé essayer de cette manière mais je n'arrive pas à en voir une
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
. Etablis une relation liant
à
et
. Ensuite trouve une fonction
vérifiant : [CENTER]
[/CENTER]