Polynomes:pas évident,mais amusant

[ffpower]

Exo au caratere bien trempé,un peu casse pied des fois mais tres sympatique dans le fond,pret a ouvrir son coeur a qui saura bien l'aborder,cherche mathématicien déterminé,aimant prendre du bon temps en longues réflexions amicales,pour relation intense a court terme(voire moyen terme)

Description:
"Trouver les polynomes P a coefficients entiers(relatifs) envoyant les carrés dans les carrés"

Qui veut tenter sa chance?

EDIT:Argh,j ai failli oublié:BONJOUR tout le monde!!Je sais pas si "énigmes" est aussi contaminé par cette histoire,mais mieux vaut prévenir que guérir..

[ThSQ]

"Trouver les polynomes P a coefficients entiers(relatifs) envoyant les carrés dans les carrés"

C'est-à-dire ? P(n²)=n² pour tout n (auquel cas je préfère mon annonce pour une blonde à forte ...) ou plutôt P(n²) est un carré pour tout n ?

[Imod]

Je ne vois toujours pas ton bonjour( un bonjour à la fin me paraît discourtois :triste: , alors je dis bonjour à ta place :we:
" Bonjour !"

Je ne voudrais pas qu'il disparaisse car je trouve ton problème intéressant même s'il me semble carrément difficile !

Je ne suis pas sûr qu'un bonjour dans un message de réponse corrige la faute initiale mais apparemment le méchant robot qui ne connaît manifestement pas les trois lois semble encore épargner ce forum :help:

Imod

[ThSQ]

Un essai, pas bien fini et sans doute louche mais boulot boulot ....

d°P est pair = 2n

P(x) = a * x^{2n} + .... = x^{2n} (a + b/x + ....)

sqrt{P(x)} = DL avec binôme (pour une fois que ces saloperies servent) = Q(x) + O(1/x)
soit avec Q un polynôme de degré n.

Si P et Q différent ils différent au moins de 2Q(x) (biscotte ce sont des carrés) impossible.

[leon1789]

C'est-à-dire ? P(n²)=n² pour tout n (auquel cas je préfère mon annonce pour une blonde à forte ...) ou plutôt P(n²) est un carré pour tout n ?

je prends en charge P(n²)=n² pour tout n
et toi l'autre , hein ? :we:

[Doraki]

Soit f(x) = P(x²)^(1/2) et supposons P de degré d.
On regarde les dérivées de f :

Pour tout n,

Soit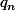 le degré de .
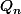En dérivant il vient que .
Comme , ,et donc .
Et donc, est un O(x^(n(2d-1)+2d((1-2n)/2))) = O(x^(d-n))

Par conséquent, .

Maintenant, soit l'opérateur de différence finie (), et regardons pour x entier.
Alors, comme tend vers 0, tend aussi vers 0.

Seulement voilà, envoie les entiers sur des entiers (comme f), et donc il s'ensuit que est stationnaire à 0.

Et là on a gagné parcequ'alors, il existe un polynôme Q de degré d tel que f(x) = Q(x) sur presque tous les entiers.
En particulier, P(x²) = Q(x)² pour presque tous les entiers.
Donc en fait, P(x²) = Q(x)² pour tout x.

Et puis là bah c'est plus très dur de montrer que P est nécessairement de la forme R(X)² ou X.R(X)²

[ffpower]

waow,comme t as torché ca direct lol,en moins d une aprem..Bon bah,félicitations quoi..Tu connaissais ou bien?(pourtant c est moi et un pote qui l avons inventé lol)

[Doraki]

Non, j'avais jamais vu..
Mais bon, on est quand même bien tenté dès le début de dire que P(x²) doit être le carré d'un polynôme.
Et puis là il faut un argument brutal vu qu'on peut à peu près rien faire dessus. Une racine carrée comme ça, ça empêche de faire tout ce qu'on aimerait faire avec des polynômes.

f a une croissance polynômiale et est à valeurs entières, donc c'est un polynôme grâce aux différences finies... ça ne m'étonnerait pas que j'aie déjà vu ce principe quelquepart, mais je l'ai oublié depuis.

[ffpower]

ok,bon bien ouej.L exo a la methode équivalante,c est:si pour tout n,n^x est entier,montrer que x est entier..

[ffpower]

Dans le meme genre:Trouver les poly a coeff entiers qui envoie les nombres premiers dans les nombres premiers.Pour celle la,j ai trouvé une démo assez courte,mais qui utilise un gros theoreme.J ai pas encore trouvé de démo élémentaire par contre(mais je pense qu il y en a une..)