Exercice niveau bac+0 bac +1 mais pas si facile

[aviateur]

Bonjour
Soit p un polynôme de degré 99 qui vérifie

Déterminer la valeur de p(100).

[LB2]

p(100)=2^100-1 ?
je serais curieux d'une méthode qui montrerait p(100)=p(0)+p(1)+....+p(99) sans passer par l'interpolation de Lagrange

[aviateur]

Bonjour
Oui c'est la bonne réponse. Vu le titre je propose une autre réponse qui n'utilise pas l'interpolation de Lagrange car elle n'est pas vraiment connue au niveau de la terminale.
Pour répondre à un niveau plus élémentaire on peut chercher une construction par récurrence.
En effet posons (cherchons) un polynôme degré n qui vérifie
C'est pas difficile de voir que
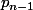
D'autre part si on su construire on voit que
Le tout est de deviner la cste
posons h_n(x)=x(x-1).....(x-n-1); on voit que h(n)=n! Pour simplifier posons H_n(x)=h_n(x)/n!
On a donc
Si on regarde la valeur de la cste pour les premières valeurs de n=1,2,3 on voit que cette constante vaut 1.
Conjecturons que cette constante soit toujours 1.
Alors et ou encore
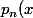
Il reste à justifier cette expression de ) et la valeur de par récurrence, ce qui facile à faire.
Pour répondre à la question on prend n=100.