Polynômes cyclotomiques pas très irréductibles

[Archytas]

Salut, petit défi sympa:
Soit un entier naturel. Soit un corps fini avec dans lequel est non nul. Montrer que le n-ème polynôme cyclotomique est irréductible dans si et seulement si la classe de engendre le groupe multiplicatif .
En déduire que et sont réductibles sur tout corps fini

[Archytas]

Petits indices :
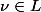
(1) Si est une racine primitive n ème (notées ) alors agit simplement transitivement sur autrement dit pour tout couple .
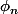
(2) Lorsqu'un corps possède une racine primitive n ème, il les possède donc toutes et ce sont exactement les racines de avec (n non nul dans L).
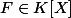
(3) Pour scindé simple dans une extension de . Si pour tout couple de racine il existe (automorphisme de L laissant les éléments de K invariants i.e. ) tel que alors irréductible dans .

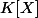
Normalement avec ça, ça devrait être plus facile ! Je mettrai le lien de l'article dans quelques jours.