Trouvez 1000 avec 4 chiffres différents (non concaténés) et vous avez le droit à + - x / ^ racine carré et factorielle.
Qui sera le premier à viser juste ? :hein:
En plein dans le mille !
10 messages
- Page 1 sur 1
Erreur Latex
Je suis peut être très naïf mais est-ce vraiment possible de déterminer toutes les solutions ?
Car chaque solution peut s'écrire de différentes façons, par exemple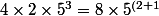}=\frac{8\times 5^3}{5}) ..
..
Après si cela est possible, j'avoue que j'aimerais bien voir à quoi ressemble l'explication ^^
Car chaque solution peut s'écrire de différentes façons, par exemple
Après si cela est possible, j'avoue que j'aimerais bien voir à quoi ressemble l'explication ^^
Waax22951 a écrit:Je suis peut être très naïf mais est-ce vraiment possible de déterminer toutes les solutions ?
Car chaque solution peut s'écrire de différentes façons, par exemple..
Après si cela est possible, j'avoue que j'aimerais bien voir à quoi ressemble l'explication ^^
Pas trop d'accord avec la seconde égalité ( à moins de remplacer le 5 du bas par 1)
Par ailleurs, s'il y a beaucoup d'écritures possibles, il n'y en a pas une infinité.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
