De minimum et maximum locaux

[Elerinna]

Voici un petit exercice d'oral posé il y a quelques années sur la notion d'un minimum relatif : à toi de te lancer !

1) Soit une application développable en série entière de rayon .
On suppose que, pour n assez grand, . Que dire de f ?

2) Soit , et U un ouvert de . Peut-il y a avoir un maximum relatif en un point z0 de U ?
On suppose U borné; soit F la frontière de U : \ .
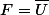
Alors montrer que :

[Le_chat]

Salut. C'est un oral posé où?

Et je dis surement une bêtise, mais la dernière inégalité à démontrer n'est pas carrément une égalité?


Spoiler pour la 2:

En effet pour l'indication on utilise que P(z)=1/2pi*integrale de P(z+r*exp(it))dt pour tout r>0.

Pour un sens de l'inegalité c'est simplement la continuité de z->|P(z)| et la compacité de F.

Pour l'autre sens on dit que l'application de U barre dans R qui à z associe |P(z)| est continue, et elle atteint son sup car U barre est compact. En vertu de l'indication, il ne peut pas être atteint sur U, donc il est atteint sur la frontière, et on a en fait égalité.

[Nightmare]

Hello,

pour la 1) f(z)=f(z/(z+1)) par le principe des zéros isolés. Doit surement y avoir moyen de déduire que f est constante, mais j'y arrive pas...

La 2) est classique.

[Le_chat]

D'ailleurs pour la 2), juste pour démontrer qu'il n'y a pas de maximum local, est-ce qu'il y a une méthode pour se passer de la formule integrale? Ça tombe parfois aux concours MP, et c'est pas du tout au programme le résultat avec l'integrale, j'aimerai connaitre une façon de le faire en respectant le programme de prépa.


Bien sur, redemontrer la formule n'est pas sorcier mais ça fait tellement parachuté...

[Doraki]

Je suppose que dans la 2, on parle d'une fonction holomorphe P définie sur un ouvert V contenant l'adhérence de U et que par maximum local on parle de maximum local du module de P ?

[ffpower]

La 1 marche bien par des Rolle successifs.

La 2 est pas très clair posée telle quelle comme le souligne Doraki.

Pour Le chat: on peut prouver l'absence de max local à la main oui: Si tu connais la démo analytique classique de D'alembert Gauss, bah c'est en gros la même chose: Si z0 est dans U, en utilisant le développement en série entière de f en z0 on écrit
(quand h tend vers 0), où a est non nul
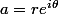
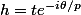
On écrit et on choisit de sorte que
(quand t tend vers 0)
Choisissant t assez petit on obtient ainsi un z tel que |f(z)|>|f(z0)|.

[Doraki]

Moi pour le 1 mon réflexe c'est plutôt dire que pour tout x dans [0;R[, f(x) = f(x/(x+1)) = f(x/(2x+1)) = f(x/(3x+1)) = ... = f(0) par continuité en 0.

[Nightmare]

Moi pour le 1 mon réflexe c'est plutôt dire que pour tout x dans [0;R[, f(x) = f(x/(x+1)) = f(x/(2x+1)) = f(x/(3x+1)) = ... = f(0) par continuité en 0.

Bien vu. :mur:

[Le_chat]

Pour Le chat: on peut prouver l'absence de max local à la main oui: Si tu connais la démo analytique classique de D'alembert Gauss, bah c'est en gros la même chose: Si z0 est dans U, en utilisant le développement en série entière de f en z0 on écrit
(quand h tend vers 0), où a est non nul
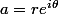
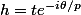
On écrit et on choisit de sorte que
(quand t tend vers 0)
Choisissant t assez petit on obtient ainsi un z tel que |f(z)|>|f(z0)|.

Ah oui très bonne idée! Merci beaucoup.

[Elerinna]

La 1 marche bien par des Rolle successifs.

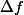
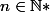
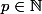
L'étude d'une suite particulière approximant pour grand et fait (aussi) converger vers la conclusion.

[Elerinna]

Je suppose que dans la 2, on parle d'une fonction holomorphe P définie sur un ouvert V contenant l'adhérence de U et que par maximum local on parle de maximum local du module de P ?

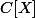
Oui. est l'ensemble des polynômes à une indéterminée à coefficients dans . :id: