Minimum d'un produit de distances.
Olympiades mathématiques, énigmes et défis
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 04 Déc 2006, 21:50
par yos » 04 Déc 2006, 21:50
Bonsoir.
Voici un exercice pour lequel je ne suis pas sûr qu'il y ait une solution type olympiade.
Dans le plan, on considère n points
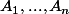
et un cercle

de rayon 1.
Démontrer qu'il existe un point M de

tel que
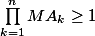
.
-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 05 Déc 2006, 01:54
par darkmaster » 05 Déc 2006, 01:54
Par récurrence:
Initilisation:
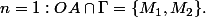
Donc, parmi
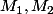
il y a un point soit
=1)
Hypothèse de récurrence:
Pour n=k, on a toujours
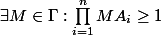
pour l'ensemble des points
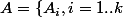
On note M :
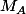
Rang(k+1):
D'abord, on a un emsemble A de (k+1) points dans le plans. On doit démonter l'existence de
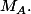
On considère les parties
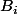
de A qui contient k points.Donc, il y a n ensembles comme ça.Alors,
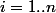
. Chaque
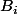
a un
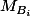
( par hypothèse de récurrence). On va montrer il éxiste un ensemble
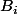
tel que:
.On appelle les points dans
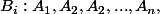
et le point
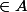
mais
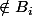
:
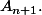
On a

-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 05 Déc 2006, 11:41
par darkmaster » 05 Déc 2006, 11:41
Tu as une solution type non-olympiade?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 05 Déc 2006, 12:26
par yos » 05 Déc 2006, 12:26
darkmaster a écrit:Tu as une solution type non-olympiade?
Oui. Je la donnerai si ça intéresse quelqu'un.
-
MikO
- Membre Relatif
- Messages: 106
- Enregistré le: 27 Nov 2006, 19:21
-
 par MikO » 05 Déc 2006, 19:17
par MikO » 05 Déc 2006, 19:17
laisse nous un peu chercher :p
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 05 Déc 2006, 20:20
par Imod » 05 Déc 2006, 20:20
On ne peut pas s'empêcher de penser au principe du maximum mais il faudrait fouiller un peu plus .
Imod
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 08 Déc 2006, 22:43
par Imod » 08 Déc 2006, 22:43
J'ai en effet trouvé une solution simple ( si on a :id: ) utilisant le principe du maximum , je vais voir maintenant si on peut voir le problème autrement .
Imod
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 08 Déc 2006, 23:22
par yos » 08 Déc 2006, 23:22
Ma solution est plus terre à terre tout de même. Tu peux nous donner la tienne si tu veux.
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 08 Déc 2006, 23:43
par Imod » 08 Déc 2006, 23:43
Je te donne ma solution demain , elle est courte mais nécessite un peu de "latex" et après 12 heures d'interruption d'électricité , je pare au plus pressé ( tempête oblige ) .
A demain ,
Imod
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 09 Déc 2006, 12:01
par Imod » 09 Déc 2006, 12:01
Il suffit de considérer le cercle trigonométrique et

points

d'affixes

. On pose
=\prod_{i=1}^n(z-a_i)})
alors
=\sum_{i=0}^nb_iz^i)
avec
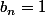
.
=\sum_{i=0}^nb_iz^{n-i})
est holomorphe sur

et
=b_n=1)
. D'après le principe du maximum
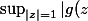|=\sup_{|z|\leq 1}|g(z)|\geq 1})
. Or pour
=z^nf(\frac{1}{z}))
donc pour
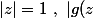|=|f(\frac{1}{z})|)
et pour finir :
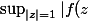|=\sup_{|z|=1}|g(z)|\geq 1})
.
Imod
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 09 Déc 2006, 14:30
par yos » 09 Déc 2006, 14:30
Salut.
Pourquoi
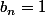
?
Ta définition de

passe du coef constant au coef dominant non?
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 09 Déc 2006, 14:36
par Imod » 09 Déc 2006, 14:36
=\displaystyle{\prod_{i=1}^{n}(z-a_i)=z^n-(a_1+...a_n)z^{n-1}+...})
Imod
PS : J'ai un peu mélangé les i et les k , je vais corriger :marteau:
PPS : L'intérêt de la fonction g est justement d'échanger les coefficients dominants et constants de f tout en gardant le même module que f sur le cercle unité.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 09 Déc 2006, 17:46
par yos » 09 Déc 2006, 17:46
C'est bien vu.
Si tu veux éviter le principe du maximum, tu peux écrire l'égalité
\overline{f(e^{i\theta})}d\theta=1+\sum_{k=0}^{n-1}|b_k|^2)
,
qui découle du fait que l'intégrale sur
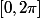
d'un terme
})
est nulle si
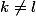
, et vaut
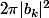
sinon.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités