Limite d'un produit
Olympiades mathématiques, énigmes et défis
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 31 Aoû 2006, 23:30
par nekros » 31 Aoû 2006, 23:30
Salut,
Soit
 \in \mathbb{R^2})
tel que
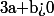
et
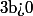
.
Déterminer
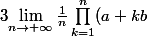^{\frac{1}{n}})
Bonne réflexion :lol4:
A+
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 01 Sep 2006, 12:51
par nekros » 01 Sep 2006, 12:51
Personne d'intéressé ?
-
andros06
- Membre Relatif
- Messages: 180
- Enregistré le: 30 Aoû 2006, 13:30
-
 par andros06 » 01 Sep 2006, 13:01
par andros06 » 01 Sep 2006, 13:01
si si calcul en cours ...
-
andros06
- Membre Relatif
- Messages: 180
- Enregistré le: 30 Aoû 2006, 13:30
-
 par andros06 » 01 Sep 2006, 13:28
par andros06 » 01 Sep 2006, 13:28
bon j'ai trouvé un résultat mais il ne me semble pas très juste :
- passage au ln
- manipulation de l'expression
- je trouve : lim = b
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Sep 2006, 13:33
par Flodelarab » 01 Sep 2006, 13:33
avec -ln(n) qui tend vers l'infini ?
bizarre
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 01 Sep 2006, 13:54
par nekros » 01 Sep 2006, 13:54
andros06 a écrit:bon j'ai trouvé un résultat mais il ne me semble pas très juste :
- passage au ln
- manipulation de l'expression
- je trouve : lim = b
Effectivement, ce n'est pas le bon résultat... :triste:
A+
-
buzard
- Membre Relatif
- Messages: 274
- Enregistré le: 22 Mai 2006, 14:29
-
 par buzard » 01 Sep 2006, 15:05
par buzard » 01 Sep 2006, 15:05
en transformant l'expression (factorisation, stirlnig et développement asymptotique d'ordre 1) j'obtient b/e
La réonse est plutôt étrange elle ne dépend pas de la valeur de a!
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 01 Sep 2006, 15:12
par nekros » 01 Sep 2006, 15:12
buzard a écrit:en transformant l'expression (factorisation, stirlnig et développement asymptotique d'ordre 1) j'obtient b/e
La réonse est plutôt étrange elle ne dépend pas de la valeur de a!
Et pourtant,
^{\frac{1}{n}}=\frac{b}{e}})
Bravo à toi donc :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités