Intégrale et fonction nulle
Olympiades mathématiques, énigmes et défis
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Juil 2006, 17:50
par Nightmare » 17 Juil 2006, 17:50
La contradiction avec quoi ? :hein:
Il n'y a aucune contradiction, c'est juste que G est en même temps positive et négative donc est nulle
:happy3:
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 17 Juil 2006, 17:50
par Mikou » 17 Juil 2006, 17:50
g decroit et et g(0) =0 dont g' inferieur a 0 donc G est decroissante.
Or pour tout x G(x) est superieur a 0 et de plus G(0) = 0 donc G est constante a 0. -> g constante a 0
On aurait dont
 \int_0^x f = 0)
soit f(x) = 0 ou on aurait F la primitive de F qui sannule en 0 On aurait donc F(x) = 0, f serait constante
on aurait
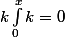
soit
 = 0)
pour tout x, soit finalement k = 0
f est donc constante a 0

-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Juil 2006, 17:53
par Nightmare » 17 Juil 2006, 17:53
Je comprends pas grand chose désolé Mikou ...
Qu'est-ce que tu entends par "g constante a 0" ?
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 17 Juil 2006, 17:57
par Mikou » 17 Juil 2006, 17:57
nightmare : on a g qui est decroissante et inferieur a g(0) = 0
-> G' inferieur a 0 -> G decroissante.
Or G(x) superieur a 0 ( carré) et G(0) = 0
-> G constante a 0
Comme G est constante G'= 0
-> g = 0 ( car G'=2g )
puis je fini de conclure avec mon precedent post
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Juil 2006, 17:59
par Nightmare » 17 Juil 2006, 17:59
Oui mais on a pas besoin de passer par G= 0 => G' =0 => g=0 => f nulle
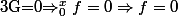
Ca suffit
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 17 Juil 2006, 18:04
par nekros » 17 Juil 2006, 18:04
Attention, il faut que f soit positive !!
Au fait j'ai terminé mon précédent post, tu ne m'avais pas laissé le temps de finir !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Juil 2006, 18:08
par Nightmare » 17 Juil 2006, 18:08
Non pas besoin de positivité, quelque soit x l'intégrale de
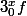
est nulle et cela n'est vrai que si f=0, pas besoin de positivité.
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 17 Juil 2006, 18:10
par Mikou » 17 Juil 2006, 18:10
oui ^^ c'est evident nightmare mais je ne savais pas le demontrer donc jai preferé prouver que f etait constante et en deduire quelle vaut 0 :p
En tous cas bien vu ton astuce :lol4:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Juil 2006, 18:13
par Nightmare » 17 Juil 2006, 18:13
Edit Moi même : Non j'avais bien raison, vu que la propriété est vraie pour tout x réel, pas besoin de la positivité de f.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 17 Juil 2006, 18:18
par nekros » 17 Juil 2006, 18:18
Pour moi,
Pour une fonction f positive et continue sur [a,b], si l'intégrale de f sur [a,b] est nulle, alors f est constamment nulle.
Ici, on veut montrer que f=0, mais on ne sait pas si f est positive.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Juil 2006, 18:23
par Nightmare » 17 Juil 2006, 18:23
Pour tout x réel,
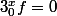
On en déduit que la dérivée de
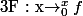
sur R est nulle, c'est à dire que f est nulle. Pas besoin de positivité.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 17 Juil 2006, 18:25
par nekros » 17 Juil 2006, 18:25
Ce n'est pas parce que la dérivée d'une fonction est nulle que cette fonction est nulle.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Juil 2006, 18:25
par Nightmare » 17 Juil 2006, 18:25
Pour tout x réel,
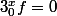
On en déduit que la dérivée de
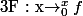
sur R est nulle, c'est à dire que f est nulle. Pas besoin de positivité.
:happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Juil 2006, 18:26
par Nightmare » 17 Juil 2006, 18:26
Je n'ai jamais dit ça Nekros
mais F est nulle, donc sa dérivée F'=f est nulle.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 17 Juil 2006, 18:28
par nekros » 17 Juil 2006, 18:28
Ah toutes mes excuses, j'ai mal lu depuis le départ...
Mais quelque chose me gêne toujours...
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 17 Juil 2006, 18:28
par Mikou » 17 Juil 2006, 18:28
nekros tu lis jms t pm ?
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 17 Juil 2006, 18:32
par nekros » 17 Juil 2006, 18:32
Désolé, lol, c'est fait !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Juil 2006, 18:36
par Nightmare » 17 Juil 2006, 18:36
Pas de problème :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
 \int_0^x f = 0) soit f(x) = 0 ou on aurait F la primitive de F qui sannule en 0 On aurait donc F(x) = 0, f serait constante
soit f(x) = 0 ou on aurait F la primitive de F qui sannule en 0 On aurait donc F(x) = 0, f serait constante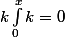 soit
soit  = 0)

