
Inéquation dans IN
33 messages
- Page 2 sur 2 - 1, 2
Re: Inéquation dans IN
c'est une bonne nouvelle ... 

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Inéquation dans IN
Est ce que la partie décimale de ta suite 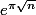 ne serait tout simplement pas dense dans [0,1] ? ça ne serait pas très étonnant étant donné sa tête et ça expliquerait qu'on trouve pas mal de valeurs aussi proches qu'on veut de 1 (ou 0 ou
ne serait tout simplement pas dense dans [0,1] ? ça ne serait pas très étonnant étant donné sa tête et ça expliquerait qu'on trouve pas mal de valeurs aussi proches qu'on veut de 1 (ou 0 ou  d'Euler si on veut)
d'Euler si on veut)
Re: Inéquation dans IN
... ou même de votre date de naissance ou de la mienne ... certainement je ne sais pas, je n'ai pas les capacités de répondre à ce type de question. Il me semble avoir lu que  pourrait être un nombre univers avec ce type de propriétés qui amusent ou fascinent les amateurs et curieux de ma trempe mais de la à faire une analogie avec les nombres de la forme
pourrait être un nombre univers avec ce type de propriétés qui amusent ou fascinent les amateurs et curieux de ma trempe mais de la à faire une analogie avec les nombres de la forme 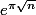 je ne m'y risquerais pas
je ne m'y risquerais pas 
Re: Inéquation dans IN
Il me semble que la notion de densité est beaucoup plus maniable que celle de nombre univers. Ce qui m'a fait pensé à ça c'est la suite sin(n). On peut montrer qu'elle est dense dans [-1,1].
D'ailleurs s'il y a des amateurs d'exponentielle complexe j'ai un énoncé qui pourrait vous occuper :
D'ailleurs s'il y a des amateurs d'exponentielle complexe j'ai un énoncé qui pourrait vous occuper :
On considère la suite de complexe.
Montrer que pourla suite est équirépartie sur le cercle unité. Est ce encore vrai pour
? Pour
?
Re: Inéquation dans IN
Je ne sais pas s'il est aussi simple de parler de densité avec les nombre de la forme 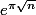 qu'avec les nombres de la forme
qu'avec les nombres de la forme ) compte tenu du fait que comme je l'expliquais à l'époque :
compte tenu du fait que comme je l'expliquais à l'époque :
"Lorsqu'on essai de réécrire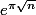 , il est possible d'obtenir quelque chose de la forme :
, il est possible d'obtenir quelque chose de la forme :
})
La fonction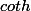 étant strictement supérieur à
étant strictement supérieur à  (asymptote horizontale) on s'attend à ce que
(asymptote horizontale) on s'attend à ce que 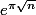 tende vers +inf mais cela ne donne aucune info sur la partie décimale de la chose."
tende vers +inf mais cela ne donne aucune info sur la partie décimale de la chose."
En cherchant sur le net, cette dernière réécriture, pourrait éventuellement faire rappeler la fonction dite de Langevin sauf que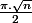 est foncièrement différent de 1
est foncièrement différent de 1 
En résumé, nous sommes en présence d'un OVNI et personne aujourd'hui ne peut prévoir le comportement de la chose.
"Lorsqu'on essai de réécrire
La fonction
En cherchant sur le net, cette dernière réécriture, pourrait éventuellement faire rappeler la fonction dite de Langevin sauf que
En résumé, nous sommes en présence d'un OVNI et personne aujourd'hui ne peut prévoir le comportement de la chose.
Re: Inéquation dans IN
Il y a le critère de Fejér :
Soit une fonction de R+* dans R dérivable et telle que
une fonction de R+* dans R dérivable et telle que
(i) est monotone
est monotone
(ii) = 0)
(iii) = \infty)
Alors la suite)) est équirépartie modulo 1 (i.e. les valeurs prises par la partie décimale de f(n) seront denses dans [0,1] et mieux encore).
est équirépartie modulo 1 (i.e. les valeurs prises par la partie décimale de f(n) seront denses dans [0,1] et mieux encore).
On peut appliquer ça à=\frac{1}{\pi}\sqrt{x}) qui vérifie les trois conditions et ça montre que
qui vérifie les trois conditions et ça montre que )) est aussi dense dans [0,1] modulo 1. (et c'est le même outil pour l'énoncé que j'ai posé au dessus, ça marche pour
est aussi dense dans [0,1] modulo 1. (et c'est le même outil pour l'énoncé que j'ai posé au dessus, ça marche pour 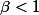 , pour
, pour 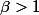 il faut utiliser le critère de Van der Corput pour tuer ce cas pour les entiers et se donner pas mal de peine pour bêta quelconque >1)
il faut utiliser le critère de Van der Corput pour tuer ce cas pour les entiers et se donner pas mal de peine pour bêta quelconque >1)
Et attention dans ton expression, si coth est minorée, ta suite est majorée or) tend vers l'infini
tend vers l'infini
Soit
(i)
(ii)
(iii)
Alors la suite
On peut appliquer ça à
Et attention dans ton expression, si coth est minorée, ta suite est majorée or
Modifié en dernier par Archytas le 04 Mar 2017, 13:19, modifié 1 fois.
Re: Inéquation dans IN
Bonjour,
Donc vous venez de démontrer que les nombres de la forme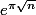 se rapprocheront aussi près que l'on souhaite d'un nombre entier mais ceci ne donne aucune indication sur la manière de choisir cet entier
se rapprocheront aussi près que l'on souhaite d'un nombre entier mais ceci ne donne aucune indication sur la manière de choisir cet entier  est ce bien cela ?
est ce bien cela ?
Donc vous venez de démontrer que les nombres de la forme
Re: Inéquation dans IN
Archytas a écrit:Il y a le critère de Fejér :
Soitune fonction de R+* dans R dérivable et telle que
(i)est monotone
(ii)
(iii)
Alors la suiteest équirépartie modulo 1 (i.e. les valeurs prises par la partie décimale de f(n) seront denses dans [0,1] et mieux encore).
On peut appliquer ça àqui vérifie les trois conditions
Bonjour,
Après relecture, il me semble que le deuxième critère n'est pas respecté dans la mesure ou
En prenant
Re: Inéquation dans IN
Archytas a écrit:Il y a le critère de Fejér :
Soitune fonction de R+* dans R dérivable et telle que
(i)est monotone
(ii)
(iii)
Alors la suiteest équirépartie modulo 1 (i.e. les valeurs prises par la partie décimale de f(n) seront denses dans [0,1] et mieux encore).
euh ça dit quoi au sujet de f(x) = 1-1/x ?
Re: Inéquation dans IN
Désolé le (iii) c'est lim xf'(x) =+infini j'édite mon post
Et anthony je l'applique juste à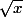 qui nous dit que sa partie décimale sera équirépartie. Ensuite on a au moins la densité de la partie décimale de
qui nous dit que sa partie décimale sera équirépartie. Ensuite on a au moins la densité de la partie décimale de 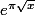 et j'imagine qu'avec un peu de boulot on peut même montrer l'équirépartition.
et j'imagine qu'avec un peu de boulot on peut même montrer l'équirépartition.
Et anthony je l'applique juste à
Re: Inéquation dans IN
Archytas a écrit:je l'applique juste àqui nous dit que sa partie décimale sera équirépartie. Ensuite on a au moins la densité de la partie décimale de
et j'imagine qu'avec un peu de boulot on peut même montrer l'équirépartition.
Bonjour Archytas,
Votre application à la fonction
En prenant
Autrement dit, il me semble que le critère de Féjer n'est pas l'outils adéquat (dans ce cas) pour démontrer l'équirépartion non ?
Re: Inéquation dans IN
Bonjour,
Plus frustrant encore, il semblerait qu'on ne sache pas si les suites de la forme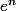 ou
ou 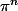 sont équidistribuées mod 1 d'après cet article : https://fr.wikipedia.org/wiki/Suite_%C3 ... ibu.C3.A9e
sont équidistribuées mod 1 d'après cet article : https://fr.wikipedia.org/wiki/Suite_%C3 ... ibu.C3.A9e
Autrement dit, j'ai bien peur qu'on ne puisse pas dire grand chose sur les nombres de la forme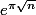
Plus frustrant encore, il semblerait qu'on ne sache pas si les suites de la forme
Autrement dit, j'ai bien peur qu'on ne puisse pas dire grand chose sur les nombres de la forme
Re: Inéquation dans IN
anthony_unac a écrit:Votre application à la fonctionne change rien au fait que :
En prenant
Autrement dit, il me semble que le critère de Féjer n'est pas l'outils adéquat (dans ce cas) pour démontrer l'équirépartion non ?
Exact oui je me suis emballé, ça ne marche pas ici... Je m'étais dit que dense composé continûment donnait un truc dense mais bon comme notre équirépartition ne donne que la densité pour la partie décimale, on a aucune chance de la récupérer pour l'exponentielle réelle (contrairement à l'exponentielle complexe qui se comporte bien puisqu'elle "tue" la partie entière des réels qu'elle mange).
Mea culpa
33 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
