Inéquation fonctionnelle II

[Zweig]

Salut,

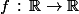
Soit , dérivable en 0 et vérifiant . Déterminer toutes les fonctions vérifiant

[CENTER][/CENTER]

Aide : On pourra résoudre le cas g(x) = 1 + x dans un premier temps.

[lol37]

Salut
Je vois que je t'ai inspiré.. :zen:
g doit être continue sur R ?

[Zweig]

Aucune hypothèse de continuité n'est imposée, seulement de dérivabilité en 0 (et g(0) = 1)

[acoustica]

Salut,

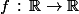
Soit , dérivable en 0 et vérifiant . Déterminer toutes les fonctions vérifiant

[CENTER][/CENTER]

Aide : On pourra résoudre le cas g(x) = 1 + x dans un premier temps.

On a envie de croire dans le cas où g(x)=1+X, que les solutions sont de la forme avec , encore faut-il montrer que ce sont les seules (ce qu'elles ne sont peut-être pas d'ailleurs).

>> Zweig, tu n'aurais pas un bon poly sur les inéquations fonctionnelles par hasard ?