Inéquation fonctionnelle

par **Zweig** » 10 Avr 2009, 20:09

Salut,

Pour changer ... Pas très difficile, mais quand même sympa :

Déterminer toutes les fonctions

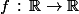
telles que pour tous

:

[CENTER]

[/CENTER]

par **lapras** » 10 Avr 2009, 20:19

fonctions constantes (théoreme gendarmes, taux d'accroissement, f'(x) = 0)

par **Mhdi** » 10 Avr 2009, 22:21

Est-ce que tu peux poster la démo complète, lapras?

par **ffpower** » 10 Avr 2009, 22:32

et tu fais tendre y vers x..

par **acoustica** » 11 Avr 2009, 19:38

Avec une petite précision dans la rédaction en utilisant la propriété suivante:
Si lim f'(x)=a quand x->b, et si f est continue en b alors f est dérivable en b et f'(b)=a

Inéquation fonctionnelle

Inéquation fonctionnelle

Qui est en ligne