
Il s'agit de déterminer la position de A, en connaissant la longueur AB=L, et sachant que (AB) passe par le coin d'un carré de 1 de coté

Ben314 a écrit:Salut,
Si A:(0,a) et b:(b,0) alors la droite (AB) a pour équation y=a-(a/b)x et elle doit passer par (1,1) donc on doit avoir 1=a-a/b, c'est à dire a+b=ab=K.
Or on doit aussi avoir L²=a²+b²=(a+b)²-2ab=K²-2K c'est à dire K²-2K-L²=0 qui permet de trouver K.
Enfin, a et b sont racine du polynôme (X-a)(X-b)=X²-(a+b)X+ab=X²-KX+K et comme on connait K, on en déduit a et b.
Effectivement c'etait plus simple que ma méthode (thales/Pythagore) ou j'ai été obligé de résoudre une equation de degrés 4
zvap a écrit: une equation de degrés 4 ( y^4+2y^3+(2-L²)+2y+1=0 )
mathafou a écrit:(d'ailleurs je ne suis pas sûr que ton équation du 4ème degré soit juste)
encore faut il définir ses inconnues .. c'est quoi lgB, ImmunoGlobuline B ?danyL a écrit:triangle OAB
OA = 1 + lgB
OB = 1 + lgA
tout dépend de ce qu'on appelle "y"danyL a écrit:on obtient bien l'équation de zvap
c'est bien ce que j'ai cru deviner en voyant tes "1+lgA"danyL a écrit:O : le point en bas à gauche du carré, ou du grand triangle si tu préfères
la longueur OA est égale à 1 (le côté du carré) plus une longueur que j'ai appelée lgA
de même pour OB
j'obtiens l'équation de zvap avec lgA comme inconnue
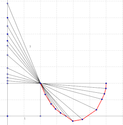
sinon on prend un compas
on trace un cercle de centre (1;1) et de diamètre L
A sera l'intersection du cercle avec l'axe vertical
comme promis, une construction possiblemathafou a écrit:figure à suivre.

mathafou a écrit:une autre façon de résoudre l'équation(en appelant K= 2 - L²)
est de remarquer que ses coefficients sont symétriques :
le coefficient deest le même que le terme constant
le coefficient deest le même que celui de Y
le terme en y² est "tout seul" (symétrique de lui-même)
pour de telles équations symétriques, si y est solution, alors 1/y aussi
(on aurait eu la même équation en x avec x = 1/y)
on peut donc la diviser par y² (après s'être assuré que 0 n'est pas solution ce qui est évident) et en réarrangeant les termes :
(y² + 1/y²) + 2(y + 1/y) + K = 0
on pose alors Z = y + 1/y et on obtient une équation du second degré en Z :
(y² + 1/y²) = (y + 1/y)² - 2 = Z² - 2
Z² -2 + 2Z + K = 0 c'est à dire Z² + 2Z - L² = 0 (ça ne te rappelle rien ?)
puis on résout l'équation du second degré en y : y + 1/y = Z
.
godzylla a écrit:sinon mathafou , il faut se mefier que l'echelle ne touche pas forcement le carre, donc les axes x et y ne sont pas forcement gradué en nombre entier

que répondre à un tel fatras .. rien !godzylla a écrit:ce serrais la capacité que nous avons de certifier qu'il existe bien une relation entre les nombres et les solutions possibles de façon a résumer cela avec une relation générique de cause a effet.
godzylla a écrit:pour l'astroide j'y ai réfléchit un peut et ce n'est pas forcement le milieu de l'échelle qui va définir la position du carre

même remarque que la première.godzylla a écrit:ça m'aide a compter les dimension et dire qu'on est sur R;) au minimum.
godzylla a écrit:je suis obligé d'utiliser y=1/ax³+ax²+a ou une de ces variante pour l'astroide.
mathafou a écrit:l'astroïde étant symétrique par rapport à la droite y = x, échange de x et y,
l'échange de x et de y dans une équation de l'astroïde donne la même équation exactement
sinon, c'est que cette équation est simplement fausse, n'a aucun rapport avec l'astroïde ...
(je ne parlerais que de maths, pas de pataphilosophie)

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :